Punktsymmetrie
Geometrie | Funktionsgraphen
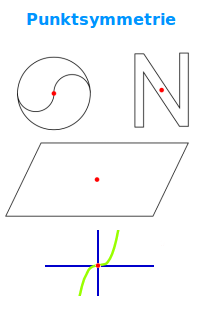
Von Punktsymmetrie spricht man, wenn eine Figur (Geometrie, Graph) an einem Punkt gespiegelt werden kann und die Figur nach der Spiegelung wieder genauso aussieht wie vor der Spiegelung. In der Fachsprache heißt das, dass die Figur auf sich selbst abgebildet wird. => Ganzen Artikel lesen …
Drehinvariant
Man nennt eine Figur punktsymmetrisch, wenn sie einen Punkt hat, um den man sie drehen kann und die Figur ist danach nicht von der Ausgangsfigur zu unterscheiden. Lies mehr zu dieser Definition unter => Punktsymmetrie
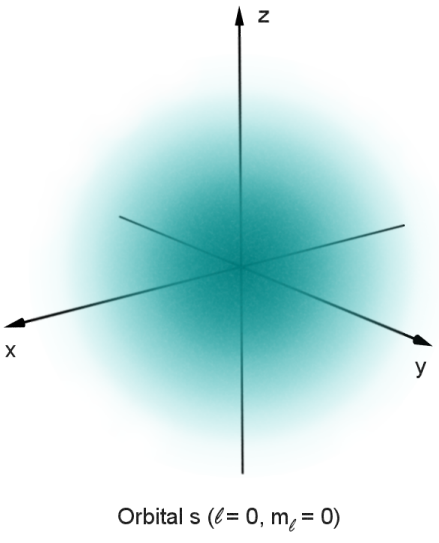
Kugelsymmetrie
… im 3D-Raum dasselbe wie => Radialsymmetrie
Physik
Von einer Zeitsymmetrie [1] oder auch einer T-Symmetrie [2] gegenüber einer Verschiebung spricht man, wenn sich ein Objekt oder ein Gesetz nicht verändert, nur weil es zu einer anderen Zeit betrachtet wird. "Bezüglich Spiegelungen in der Zeit" ist ein Gesetz symmetrisch, wenn es "rückwärts wie vorwärts" abläuft. [1] Diese Zeitsymmetrie ist näher erklärt im Artikel => T-Symmetrie
… wie f(x)=Siehe unter => Punktsymmetrie von Graphen
Punktachsensymmetrie
Beispiel
Sowohl punkt- als gleichzeitig auch achsensymmetrisch: ein Funktionsgraph, der sowohl Punktsymmetrisch zum Koordinatenursprung als auch achsensymmetrisch zur y-Achse ist der Graph von f(x)=0, also die => Nullfunktion
… z. B. wie f(x)=Siehe unter => Punktsymmetrie von Graphen
… das passt auf f(x)=0, also die => Nullfunktion
… wie f(x)=Siehe unter => Punktsymmetrie von Graphen
Im Bezug auf Graphen oft zweideutig verwendet
Der Begriff Punktsymmetrie wird in der Schulmathematik oft synonym für die Symmetrie eines Funktionsgraphen zum Koordinatenursprung (0|0) verwendet. Diese Verkürzung deckt aber nicht alle möglichen Bedeutungen des Wortes ab. Das wird hier kurz erläutert. => Ganzen Artikel lesen …
… z. B. wie f(x)=Siehe unter => Punktsymmetrie von Graphen
… am Punkt (0|0) gespiegelt, mehr unter => Punktsymmetrie von Graphen
Siehe auch
=> Punktsymmetrie von Graphen
… z. B. wie f(x)=Siehe unter => Punktsymmetrie von Graphen
… z. B. wie f(x)=Siehe unter => Punktsymmetrie von Graphen
… am Punkt (0|0) gespiegelt, mehr unter => Punktsymmetrie von Graphen
Für Figuren
Punktsymmetrie, auch Zentralsymmetrie genannt, heißt: man hat eine Figur (2D oder auch 3D) und kann für diese Figur einen Punkt finden, um den gedreht die Figur anschließend wieder genauso aussieht wie vorher. Gibt es einen solchen Punkt, ist die Figur punktsymmetrisch, anonsten nicht. => Ganzen Artikel lesen …
… Aufgaben zum Erkennen unter => pdf
… z. B. wie f(x)=Siehe unter => Punktsymmetrie von Graphen
… am Punkt (0|0) gespiegelt, mehr unter => Punktsymmetrie von Graphen
Punktsymmetrie von Graphen
Übersicht
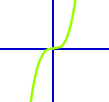
Wie für irgendeine Figur aus der Geometrie gilt auch für Graphen von Funktionen: wenn der Graph irgendeinen Symmetriepunkt hat, dann nennt man ihn punktsymmetrisch. Wenn dieser Symmetriepunkt der Ursprung (0|0) des Koordinatensystems ist, dann ist die entsprechende Funktion zusätzlich auch eine gerade Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
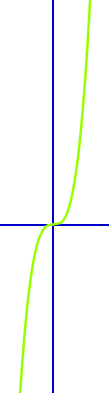Punktsymmetrie von Graphen überprüfen
Bedeutung | Methoden
Graphisch und rechnerisch: hier werden Methoden vorgestellt, wie man für eine gegeben Funktionsgleichung überprüft, ob der Graph punktsymmetrisch zu (0|0) ist. => Ganzen Artikel lesen …
