f(x)=x³ gibt abgeleitet f'(x)=3x²
Als Potenzfunktion bezeichnet man jede Funktion die man in die Form f(x)=a·x^r bringen kann. Die Definition welche Werte für r erlaubt sind ist nicht einheitlich. Für die Ableitungsregeln ist das aber unerheblich. Das kleine a darf jede beliebige reelle Zahl außer der Null sein. Zum Ableiten zieht man den Exponenten (die Hochzahl) als Faktor vor das x. Dann vermindert man den Exponenten um eins (rechnet ihn also minus eins). Die Zahl für a bleibt dabei unverändert erhalten. Aus x² wird so 2x. => Ganzen Artikel lesen …
f(x) = a·xⁿ
f(x) = 2x³ ist eine typische Potenzfunktion: als Potenzfunktion im engeren Sinn bezeichnet man jede Funktion, die man umformen kann in f(x) = Zahl·xⁿ. Das Dach ^ steht für hoch. Für das kleine n gibt es je nach Autor verschiedene Definitionen. Es steht jedoch immer für irgendeine Zahl (nie mit einer Variablen) außer der Zahl 0. Die 0 ist als Exponent nie erlaubt. Das ist hier näher vorgestellt. => Ganzen Artikel lesen …
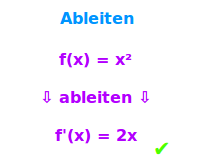Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
f(x) = a·xⁿ
f(x) = 2x³ ist eine typische Potenzfunktion. Um sie aufzuleiten erhöhte man den Exponenten (die Hochzahl) um eins. Aus hoch-drei wird dann hoch-vier. Dann multiplziert man den ursprünglichen Funktionsterm noch mit 1 durch die neue Potenz, hier also mit 1/4. Die Aufleitung ist also F(x)=(1/4)·a^4. Die Grundidee dahinter ist das => Aufleiten über Potenzregel
Zum Beispiel f(x)=4x³-2x²+8x-15 wird abgeleitet f'(x)=12x²-4x+8
Polynomfunktion ist ein anderes Wort für eine ganzrationale Funktion. Die Idee zum Ableiten besteht darin, dass man die einzelnen Glieder des Funktionstermes einzeln ableiten kann. Siehe dazu => ganzrationale Funktion ableiten
f'(x) = cos(x)
Die elementare Cosinusfunktion f(x) = cos(x) abgeleitet gibt f'(x) = -sin(x). Enthält das Argument einen komplexeren Term, benutzt man noch die Kettenregeln: f(x) = cos(4x²-8x) gibt abgeleitet f'(x) = -(8x-8)·sin(4x²-8x). Lies mehr dazu unter => Ableiten über Kettenregel
Beispiele
f(x)=x oder f(x)=3x² oder auch f(x)=0,5x³ sind Potenzfunktionen der allgemeinen Form f(x) = a·xʳ. Je nachdem welche Zahlen für den Exponenten (Hochzahl) von x eingesetzt werden dürfen, unterscheidet man drei Arten von Potenzfunktion. Für alle drei Arten stehen hier konkrete Beispiele. => Ganzen Artikel lesen …
Einsfunktion ableiten
f(x)=1 gibt abgeleitet f'(x)=0
Die Einsfunktion ist ein Sonderfall einer konstanten Funktion. Die Funktionsgleichung ist f(x)=1. Die Lösungsidee zur Ableitung ist es, die Funktion zu schreiben als f(x)=1·x⁰. Das x⁰ gibt als Wert immer 1. Man kann die Funktionsgleichung dann => ableiten über Potenzregel
