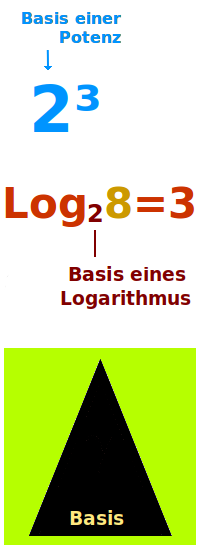Basis

Mathematik

Als Basis bezeichnet man ganz allgemein Dinge, die unten sind. Bei der Potenz 2³ ist die Zahl 2 entsprechend die Basis, nämlich die Zahl, die unten steht. Von einer Basis spricht man zum Beispiel auch bei Logarithmen, Dreiecken, Trapezen, Geodreiecken, Vektoren oder ganzen Weltbildern. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …

Subtrahieren

Abziehen

Als Subtrahieren bezeichnet man das Minusrechnen: Man hat eine gegebene Anzahl und zieht davon etwas ab. Das Ergebnis sagt, wie viel am Ende noch übrig ist. Das, was man am Anfang hatte, heißt Minuend (wird weniger gemacht), das was abgezogen wird ist der Subtrahend. Das Ergebnis nennt man die Differenz (Unterschied). Mehr dazu steht unter => Subtraktion

5: Potenz mit gleicher Basis subtrahieren

… so etwas wie 2³-2² => Potenzen mit gleicher Basis subtrahieren

6: Potenzen gleicher Basis subtrahieren

… siehe unter => Potenzen mit gleicher Basis subtrahieren