Wo
Als Ort bezeichnet man heute einen festen Punkt „in einem Raum, einem Gelände oder auf der Erdoberfläche“ [1]. In der Physik gibt man einen Ort meist an über Koordinaten [2]. Die ursprüngliche Bedeutung beinhaltet noch die Idee von etwas Letztem [3], was sich in der Bergmannsprache in Begriffen wie wie Ortsbrust oder vor Ort erhalten hat [4]. In der Geometrie ist der Ort eine Menge von Punkten, die eine Gleichung löst [5]. Zur heutigen Bedeutung, insbesondere im Sinn der Physik, siehe den Artikel zu => Ort (Physik)
… in der Physik eine Abkürzung für die => Allgemeine Relativitätstheorie
… in der Seefahrt die Abkürzung für eine => Bruttoregistertonne
… in der Medizin eine => Magnetresonanztomographie
… die kleinstmögliche Sinneinheiten, siehe auch => Worte
Mehrzahl von Wort
Mach nicht so viele Worte. Oder: seine letzten Worte waren eine Mahnung an die Zukunft: die Mehrzahl „Worte“ wird eher für Äußerungen, Aussprüche, Beteuerungen, Erklärungen, Begriffe, ganze Zusammenhänge oder bedeutsame einzelne Wörter gebraucht: => Ganzen Artikel lesen …
Offizielle Kanäle für die Datenkommunikation in Compternetzwerken
Auf UNIX-artigen Betriebssystemen darf nur das Root-Konto Dienste betreiben, die auf Ports unter 1024 liegen. Hier, im Bereich der sogenannten System Ports oder auch well-known ports, ist die höchste Konzentration an offiziellen und bekannten Ports zu finden. => Ganzen Artikel lesen …
Technischer Fachbegriff [Bergbau]
Wie schnell oder viel Wertmineral in einer Zeit gewonnen wurde => Ganzen Artikel lesen …
… 9;8;7;6;5;4 und so weiter: wird von links nach rechts immer kleiner => absteigend
8+3+2+1 = 14
Summe, Summand, Addition, Augend, Addend und noch einige mehr: die Fachworte werden hier kurz erklärt. Kurze Aufgaben dazu stehen unter => qck
… Die Worte, die man kennt und auch selbst benutzt => Wörterbücher
Mathematiker
Whitehead lebte von 1861 bis 1947. Geboren wurde er im englischen Ramsgate, er starb in Massachusetts, in den USA. Berühmt wurde er mit seinem Werk „Principia Mathematica“, das er gemeinsam mit seinem Schüler Bertrand Russel verfasste. Darin versuchten die beiden, die Mathematik ganz in der Logik zu gründen. Whitehead kritisierte auch das damalage englische Bildungssystem. 1924 ging er als Professor in die USA, wo er sich seinen philosophisch-metaphysischen Interessen widmete. Siehe auch => Alfred North Whitehead (Zitate)
Zitate von Whitehead rund um Wissenschaft
- => Whiteheadsche Kohärenz
… die Logik störende Begriffe in Mathematik etc. siehe unter => Alogismen
ist richtig geschrieben. Eine häufige Falschschreibung ist: armortisieren
… meint dasselbe wie => umgekehrt proportional
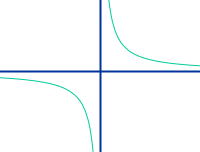Antiproportionale Funktion
… meint dasselbe wie => umgekehrt proportionale Funktion
… x steht im Nenner, z. B. f(x)=4/x, siehe unter => umgekehrt proportionale Funktion ableiten
Antiproportional heißt dasselbe wie umgekehrt proportional. Die Kernidee zum Ableiten ist, dass 1/x dasselbe ist wie x-hoch-minus-eins: 1/x = x-hoch-minus-eins ⭢ ableiten ⭢ -1 mal x-hoch-minus-zwei. Mehr dazu unter => Umgekehrt proportionale Funktion ableiten
… siehe unter => umgekehrt proportionale Gleichung aus Versuch
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => umgekehrt proportionale Gleichung aus Versuch
Mathematik
Wenn x·y immer gleich 20 sein soll, also x·y=20 gelten soll dann sind x und y zueinander antiproportional. x=2 und y=10 würde hier zum Beispiel die Gleichung lösen. Wenn man nun x doppelt so groß macht, wie es vorher war, und dabei gleichzeitig y halb so groß, dann geht die Gleichung immer noch auf: x=4 und y=5 geben malgerechnet auch 20. Statt antriproportional sagt man auch umgekehrt proportional. Siehe mehr zu diesem Thema im Artikel => umgekehrt proportionale Zuordnung
… meint dasselbe wie => Umgekehrt proportionaler Dreisatz
Mathematik
1 und 6, 2 und 3, 4 und 1,5: zwei Größen sind zueinander indirekt proportional, wenn ihr Produkt (Malrechnung) immer dasselbe Ergebnis ergibt. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
… in der Mathematik dasselbe wie die => Antiproportionalitätskonstante
Mathematik
Bei einer antiproportionalen Zuordnung oder Funktion, auch umgekehrt proportional genannt, ergeben zwei einander zugeordnete Zahlen malgerechnet immer dasselbe Ergebnis. Man spricht auch von Produktgleichheit. Dieses immer gleiche Produkt ist die Antiproportionalitätskonstante. Das ist hier mit einem Beispiel kurz vorgestellt. => Ganzen Artikel lesen …
Apfelsorten
Liste bekannter Apfelsorten
- => Boskoop [Winterapfel]
Mathematik
Als arithmetische Proportion bezeichnet man zwei Differenzen, die man gleichgesetzt hat [1]: 12-8=5-5 ist ein typisches Beispiel [3]. Seit der Nachkriegszeit (ab etwa 1945) wurde der Begriff zunehmend weniger verwendet [9]. Siehe mehr unter => Proportion
Übersicht
Man unterscheidet Istopope, Nuklide und chemische Elemente. Es gibt verschiedene Kriterien, um Atomsorten zu bilden. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
… a, b, c, d, etc. wird von links nach rechts größer => aufsteigend
Definition und Vorteile
Ein außerschulischer Lernort bietet Möglichkeiten, eigenständig oder unter Anleitung sich Wissen anzueignen oder neue Fertigkeiten zu erlernen. Typische Beispiele sind Museen, Musikschulen, Schülerlabore oder Lernwerkstätten. => Ganzen Artikel lesen …
AutoGyro MTOsport
Ein Tragschrauber, vor allem für Sportflieger
Der MTOsport ist eine Weiterentwicklung des Vorgängermodells HTC MT-03 – des ersten in Deutschland zugelassenen Ultraleicht-Tragschraubers – der Herstellerfirma HTC, aus der die Firma AutoGyro hervorging. Er zählt zur Familie der Luftsportgeräte und ist ein zweisitziges Fluggerät in Tandemanordnung. Das maximale Abfluggewicht liegt laut deutschem Gesetzgeber bei 450 kg. => Ganzen Artikel lesen …
Compiler für Fortran Programmiersprache
gfortran -ffree-form file.f: versucht file.f als Fortran Quellecode zu interpretieren. Falls das glückt, wird eine Ausgabe (Objekt)-Datei erzeugt. Ihr Name ist standardmäßig a.out. Diese kann ausgeführt werden. => Ganzen Artikel lesen …
