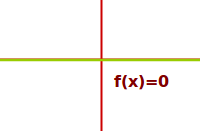
Nullfunktion
f(x)=0
Ordnet jedem x-Wert die Zahl 0 als Funktionswert zu. Der Graph ist identisch mit der x-Achse. => Ganzen Artikel lesen …
Physik
Der Begriff der Weltfunktion wurde spätestens 1912 von dem Physiker Gustav Mie gebraucht. Sie bezeichnet eine Mathematik, die die Maxwellschen Gleichungen der Elektrodynamik mit den Folgerungern von Einsteins Relativitätstheorie und der Materie verbindet und war über zwei Jahrzehnte eine Art Forschungsprogramm für andere Physiker und Mathematiker wie Max Born, David Hilbert [2] oder Ernst Reichenbächer [3]. Ein dabei wichtiger Gedanke ist die Idee der => Wirkung (Physik)
Optimierung
Eine Funktionsgleichung mit nur einer unabhängigen Variablen: die Zielfunktion ZF spielt bei sogenannten Optimierungs- oder Extremwertaufgaben eine wichtige Rolle. Im Englischen spricht man auch von einer „fitness function“. Das ist hier im Sinn von Optimierungsfunktionen kurz erklärt. => Ganzen Artikel lesen …
… f(x)=0, x-Achse als Graph, mehr dazu unter => Nullfunktion
… in der Stochastik dasselbe wie eine => Zufallsgröße
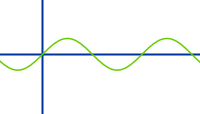Sinusfunktion
=> Ganzen Artikel lesen …
Aufhebung, Unwirksam-Machung (im Rechtswesen)
… also von f(x)=0, steht unter => Nullfunktion ableiten
… also von f(x)=0, steht unter => Nullfunktion ableiten
f(x) = 0
Die Nullfunktion ordnet jedem x-Wert als y-Wert die Zahl 0 zu. x=14 hat y=0, genauso wie auch x=999 oder x=-3. Die Nullfunktion ist ein Sonderfall einer konstanten Funktion. Siehe auch => konstante Funktion
… also von f(x)=0, steht unter => Nullfunktion ableiten
… also von f(x)=0, steht unter => Nullfunktion ableiten
… also von f(x)=0, steht unter => Nullfunktion ableiten
… also von f(x)=0, steht unter => Nullfunktion ableiten
f(x)=0
f(x)=0 nennt man die Nullfunktion. Ihr Graph ist deckungsgleich mit der x-Achse. Obwohl die Nullfunktion zu den konstanten und damit zu den ganzrationalen zählt, ist es nicht möglich, ihr eindeutig einen Grad zuzuordnen. Hier steht kurz der Grund und verschiedene Handhabungen dazu. => Ganzen Artikel lesen …
… meistens minus unendlich, siehe auch => Grad einer konstanten Funktion
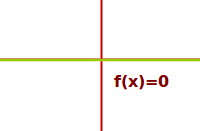Nullfunktion ableiten
f(x)=0 ergibt abgeleitet f'(x)=0
Die Nullfunktion hat als Graphen sozusagen die x-Achse. Der Graph verläuft überall waagrecht und hat damit auch für alle x-Werte die Steigung 0. Entsprechend muss die Ableitungsfunktion für alle x-Werte die Zahl 0 ergeben. Es gilt also f(x)=0 ergibt abgeleitet f'(x)=0. => Ganzen Artikel lesen …
… also von f(x)=0, steht unter => Nullfunktion ableiten
Anleitung
Die Nullfunktion f(x)=0 aufgeleitet gibt F(x)=0+C. Das große C ist die sogenanne Integrationskonstante und steht für eine beliebge Zahl, die man sich aussuchen kann. Jeder Funktion F(x)=Zahl ist abgeleitet f(x)=0 und ist daher eine Stammfunktion von f(x). => Ganzen Artikel lesen …
… also von f(x)=0, steht unter => Nullfunktion ableiten
Definition
f(x)=0 ist die sogenannte Nullfunktion. Sie besteht sozusagen nur aus Nullstellen: für jeden x-Wert erhält man als Funktionswert f(x) die Zahl 0. Also ist jeder mögliche x-Wert auch eine Nullstelle. Siehe auch => Nullfunktion
… gibt 0, mehr unter => 0 aufgeleitet
Graph
Der Graph der Nullfunktion f(x) = 0 ist sowohl achsen- wie auch punktsymmetrisch. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
… ist immer und nur der Punkt (0|Siehe unter => Nullfunktion
