Umwandlung
Man hat f(x) = x²+px+q gegeben und sucht f(x) = a(x-d)²+e. Hier ist Schritt-für-Schritt erklärt, wie man das mit Hilfe der sogenannten quadratischen Ergänzung umwandelt. => Ganzen Artikel lesen …
Analysis: standardisierte Form einer Gleichung
Gleichungen, etwa von Geraden oder Parabeln, kann man oft in verschiedenen Formen schreiben. Die am häufigsten gewählte Form nennt man oft die Normalform. Beispiel sind die Normalform der Geradengleichung y=mx+b oder die Normalform der parabelgleichung (quadratische Funktion) y=ax²+bx+c. Weitere Beispiele stehen unter => Normalformen
Übersicht
In als das Element Indium oder die Umwandlung einer Zahl oder Einheit in eine andere Art: das Wort in hat verschiedene Bedeutungen. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
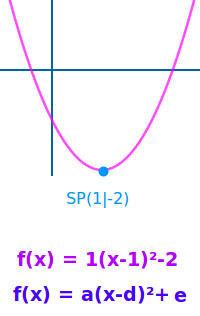Scheitelpunktform
f(x) = a·(x-d)² + e
Von quadratische Funktionen und Parabeln: aus der Scheitelpunktform y oder f(x) = a·(x²-d)²+e kann man leicht den Scheitelpunkt, die Öffnung und den y-Achsenabschnitt ablesen einer Parabel in einem xy-Koordinatensystem ablesen. Umgekehrt kann man sie leicht aufstellen, wenn man von einer Parabel den Scheitelpunkt SP und irgendeinen weiteren Punkt kennt. Das ist im Folgenden beschrieben. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Scheitelpunktform in Normalform
… Rechenbeispiel unter => Faktorisierte Form in Scheitelpunktform
… Rechenbeispiel unter => Scheitelpunktform in Normalform
… Umwandlung von quadr. Funktionen, siehe => Normalform in Scheitelpunktform
… siehe unter => Normalform in Scheitelpunktform
