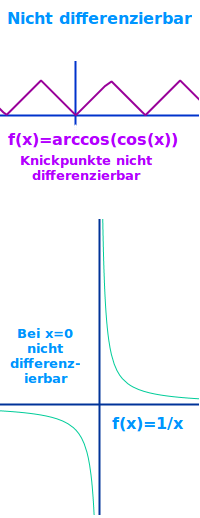
 Nicht differenzierbar
Nicht differenzierbar
Meint: man kann keine Ableitung bilden.
Differenzieren heißt ableiten, also f'(x) bilden. Nicht jede mathematische Funktion ist an allen Stellen differenzierbar: an Ecken, Lücken und Sprüngen kann man zum Beispiel keine Ableitung bilden. Anschaulich heißt das: an einem Punkt lässt sich nicht eindeutig eine Tangente anlegen. => Ganzen Artikel lesen …
 Nicht
Nicht
Mathematik
Nicht-rund, nicht-künstlich oder nicht-flach: das Wort Nicht steht in der Mathematik meist für die Idee einer direkten Verneinung, also das logische Gegenteil. Mehr zur Idee des logischen Gegenteils unter => logisches Nicht
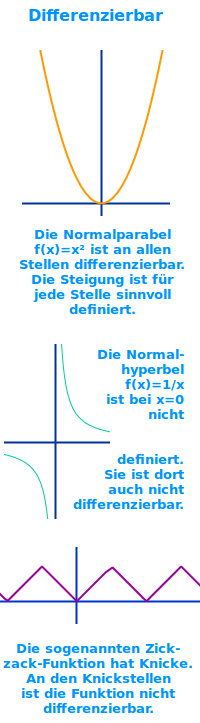 Differenzierbar
Differenzierbar
Eine Funktion kann abgeleitet werden
Differenzieren ist in der Analysis ein anderes Wort für ableiten, also f'(x) bilden. An Stellen, wo dies für eine Funktion möglich ist, ist die Funktion differenzierbar. Kann man keine erste Ableitung bilden, ist die Funktion dort nicht differenzierbar. Das ist ist hier näher erklärt. => Ganzen Artikel lesen …
… Stelle ohne eindeutige Steigung => Nicht differenzierbar
Didaktik
Binnendifferenzierung heißt in der Didaktik, dass auf verschiedene Lernbedürfnisse einzeler Schüler innerhalb einer Gruppe eingegangen wird. Als Alternative können Schüler unterschiedlicher Bedürfnisse auch auf unterschiedliche Klassen oder Schultypen verteilt werden. Siehe zum Beispiele => Binnendifferenzierung Dyskalkulie und Mathematik
Analysis
Differenzierbarkeit heißt so viel wie Ableitbarkeit: eine Funktion f(x) kann differenzierbar sein oder auch nicht. Differenzierbar heißt, dass man für alle Punkte des Graphen eine sinnvolle Steigung definieren kann. Rechnerisch heißt das: die h-Methode geht für alle x-Werte auf. Graphisch heißt es, dass man an alle Punkte des Graphen sinnvoll eine Tangente anlgegen kann. Eine ausführliche Erklärung steht unter => differenzierbar

