 Nachbarzehner
Nachbarzehner
Grundschule
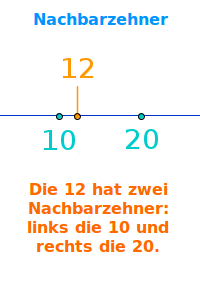
Die 12 hat zwei Nachbarzehner, die 10 und 20: jede Zahl hat immer zwei Nachbarzehner. Der linke Nachbarzehner ist kleiner als die Zahl, der rechte Nachbarzehner ist größer als die Zahl. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… siehe unter => Nachbarzehner
 Nachbareiner
Nachbareiner
Grundschule
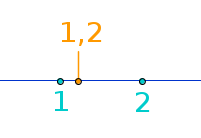
Die 3,4 hat als Nachbareiner die 3 und die 4: jede Zahl hat zwei Nachbareiner. Es sind die nächstliegenden ganzen Zahlen nach links und nach rechts auf der Zahlengeraden. Nachbareiner kann man immer ohne Komma schreiben. Nachbareiner dürfen auch negativ oder die Zahl 0 sein. => Ganzen Artikel lesen …
Definition
4,1 und 4,3 sind die Nachbarzehntel der Zahl 4,2: als Zahl in Zehntel-Schreibweise nennt man eine Zahl mit zwei Nachkommastellen. Der linke Nachbar ist die erste kleinere solche Zahl, das rechte Nachbarzehntel die erste größere solche Zahl. Dazu stehen hier Beispiele. => Ganzen Artikel lesen …
Grundschulrechnen
Uneinheitliche Handhabung bei fehlender Definition: der Begriff Nachbarzehner wird in der Grundschulmathematik verwendet. In der höheren (Hochschul) Mathematik spielt er keine Rolle. Dort spricht man von Vorgängern und Nachfolgern. Der Begriff Nachbarzehner wird aber nicht einheitlich verwendet. Es gibt widersprüchliche Deutungen. => Ganzen Artikel lesen …
Sind die 0 und die 20
Ein Zehner ist eine Zahl mit einer 0 am Ende (aber ohne Komma!). Für jede Zahl gibt es einen Zehner der kleiner ist als diese Zahl und einen der größer ist. Diese zwei Zehner nennt man die => Nachbarzehner
Sind die 10 und die 30
Ein Zehner ist eine Zahl mit einer 0 am Ende (aber ohne Komma!). Für jede Zahl gibt es einen Zehner der kleiner ist als diese Zahl und einen der größer ist. Diese zwei Zehner nennt man die => Nachbarzehner
… sind die 10 und die Siehe unter => Nachbarzehner

