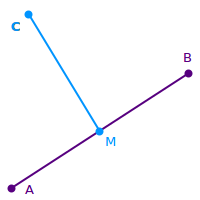
 Mittelsenkrechte
Mittelsenkrechte
Geometrie
Eine Gerade, die senkrecht, das heißt mit einem Winkel von 90 Grad, auf der Mitte einer anderen Strecke steht ist die Mittelsenkrechte dieser Strecke. Das ist hier weiter erklärt. => Ganzen Artikel lesen …
… siehe unter => Mittelsenkrechte
… heißt in der Mathematik => rechter Winkel
Beispiele
Ein Mittelpunkt ist gleich weit entfernt von den Rändern eines Objektes. Strecken, Kreise oder Kugeln haben zum Beispiel einen Mittelpunkt. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Wie Dicht etwas wäre, wenn es homogen wäre
Ein Stück Holz kann an verschiedenen Stellen unterschiedlich dicht sein. Am Rand würde ein Kubikzentimeterstückchen vielleicht viel weniger wiegen als dort, wo ein Ast in den Stamm geht. Wenn man aber so tut, als ob irgendetwas überall wäre, dann sagt man, dass die Sache homogen ist. Die Dichte von einer homogenen Sache wäre dann die mittlere Dichte. => Ganzen Artikel lesen …
 Senkrechte
Senkrechte
Etwas mit 90°-Winkel
Ein Sendemast ragt zum Beispiel als Senkrechte in den Himmel: eine Gerade, Strecke oder Ebene kann eine Senkrechte zu etwas anderem sein. Das heißt, es gibt einen rechten Winkel (90°). Verschiedene Fälle, die dabei auftreten können sind ausführlicher erklärt in dem Artikel => Orthogonale
Anleitung
Konstruieren heißt: mit Lineal und Zirkel zeichnen. Hier steht eine kurze Schritt-für-Schritt Anleitung dazu. => Ganzen Artikel lesen …
gibt es für mehrere Figuren und Körper
- => Schnittpunkt der Mittelsenkrechten im Dreieck
Geometrie
Der Schnittpunkt der Mittelsenkrechten in einem Dreieck ergibt immer den den Mittelpunkt des Umkreises. Der Umkreis ist der einzige Kreis, der genau durch alle drei Ecken des Dreiecks geht. Das ist hier näher erklärt. => Ganzen Artikel lesen …

