Statistik | Analysis
Im Zusammenhang mit Funktionsgraphen ist ein Maximum der größte y-Wert in seiner Umgebung. Man unterscheidet absolute (globale) und relative (lokale) Maxima. In der Statistik ist ein Maximum die größte Zahl einer Zahlenliste. => Ganzen Artikel lesen …
Mathematik | Statistik | Physik
Maxima (Mehrzahl von Maximum) treten in der Mathematik zum Beispiel als y-Werte von Hochpunkten auf. In der Statistik sind es einfach die größten Zahlenwerte. In der Physik gibt es zum Beispiel Maxima bei Interferenzmustern. Beides wird hier kurz erklärt. => Ganzen Artikel lesen …
Höchstens
Stromleitungen in einem Haushalt sind normalerweise für maximal 16 Ampere Stromstärke ausgelegt. Das heißt: durch die Leitungen können 4 Ampere, 12 Ampere oder auch 16 Ampere Strom fließen, aber nicht mehr. 17 Ampere sind nicht möglich. Mathematisch heißt maximal so viel wie kleiner oder gleich. Umgangssprachlich maximal dasselbe wie => höchstens
Statistik | Analysis
In der Statistik ist ein Minimum der kleinste von verschiedenen Werten. In der Analysis (Funktionsgraphen) ist ein Minimum der kleinste y-Wert eines bestimmten Bereiches. => Ganzen Artikel lesen …
Definition
Das Datenmaximum ist die größte Zahl aus einer Liste von Zahlen. Das Datenmaximum der Zahlen 12, 4 und 9 ist die Zahl 12. Hier stehen noch einige Beispiele dazu. => Ganzen Artikel lesen …
… der höchste Wert im Definitionsbereiche, dasselbe wie => globaler Hochwert
… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
Analysis
Das globale Maximum ist der y-Wert vom absoluten (globalen) Hochpunkt: erst den absoluten (globalen) Hochpunkt berechnen. Dann davon den y-Wert nehmen. Das ist dann der absolute Maximalwert oder das sogenannte globale Maximum. Eine Anleitung dazu steht unter => Globalen Extrempunkt berechnen
… heißt in der Statistik => Spannweite
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
Größte Zahl
Ein Datenmaximum ist immer die größte Zahl aus einer Liste von Zahlen. Siehe als beispielhafte Anwendung dazu => Datenmaximum bestimmen
Statistik
0,85 - 0,98 - 1,02: drei Zahlen als Daten, das Maximum der Daten ist die 1,02. Das Datenmaximum ist immer die größte Zahl aus einer Zahlenliste. Dazu stehen hier noch Beispiele. => Ganzen Artikel lesen …
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
… heißt in der Statistik => Spannweite
… heißt in der Statistik => Spannweite
… heißt in der Statistik => Spannweite
… heißt in der Statistik => Spannweite
Globales Maximum
Analysis
Der größte y-Wert in einem Definitionsbereich, also der y-Wert von einem globalen Hochpunkt ist das globale Maximum. Eine genaue Definition steht im Artikel => globaler Hochwert
y-Wert
Das globale Maximum ist der höchste, also der größte y-Wert einer Funktion: erst den globalen Hochpunkt berechnen. Dann davon den y-Wert nehmen. Das ist das globale Maximum. Eine Anleitung steht unter => Globalen Extrempunkt berechnen
y-Wert
Das globale Maximum ist der höchste, also der größte y-Wert einer Funktion: erst den globalen Hochpunkt berechnen. Dann davon den y-Wert nehmen. Das ist das globale Maximum. Eine Anleitung steht unter => Globalen Extrempunkt berechnen
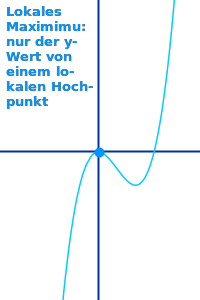Lokales Maximum
Definition
Der y-Wert oder die Stelle auf der y-Achse, die zu einem lokalen Hochpunkt gehört nennt man ein lokales Minimum. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
… Testverfahren, zur Erkennung einer => Normalverteilung
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
Übersicht
Ein Maximum in der Statistik ist die größte Zahl aus einer Liste von Zahlen. Im Zusammenhang mit Graphen und Funktionen ist ein Maximum der y-Wert von einem Hochpunkt. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
… Hochpunkte über erste Ableitung, siehe => Hochpunkte bestimmen
… heißt in der Statistik => Spannweite
In der Mitte
Von einem Maximum nullter Ordnung spricht man zum Beispiel im Zusammenhang mit dem Doppelspaltexperiment. Es ist dort das Maximum in der Mitte des Schirmes. Es hat im Vergleich zu den anderen Maxima immer den größten Werte. Mehr dazu unter => Doppelspalt-Maxima
… z. B. für Boxplots, siehe unter => Datenmaximum bestimmen
