Krümmungsmaß
Funktionsgraphen
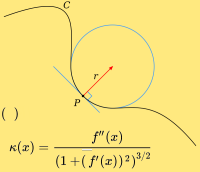
Das Krümmungsmaß für einen Punkt auf einem Graphen einer Funktion ist definiert als der Kehrwert des Radius des Anschmiegekreises oder Krümmungskreises an diesen Punkt. Diese Krümmung κ ist nicht identisch mit der zweiten Ableitung einer Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… für Graphen, siehe unter => Krümmungsmaß
Geometrie
Der Krümmungsradius einer Linie ist der „Radius eines Kreises von gleicher Krümmung wie sie die Kurve an dem betreffenden Punkte besitzt [1]“. Der Krümmungsradius spielt unter anderem eine Rolle für die zweite Ableitung f''(x) sowie auch in Einsteins allgemeiner Relativitätstheorie. => Ganzen Artikel lesen …
Krümmung
Graphen
Gibt an, ob ein Funktionsgraph von links nach rechts gehend eine Links- oder Rechtskurve macht. Die Stärke der Krümmung spielt keine Rolle, nur die Richtung. Die Berechnung erfolgt über die zweite Ableitung f''(x). => Ganzen Artikel lesen …
