Hyperbel
Graph
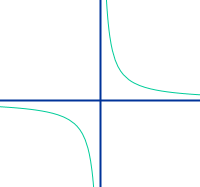
Eine Hyperbel ist der Graph einer umgekehrt proportionalen Funktion. Der Graph ist zweigeteilt und hat immer eine Definitionslücke. Daneben gibt es auch noch Hyperbeln höherer Ordnung. => Ganzen Artikel lesen …
Arten
Hyperbeln sind die Graphen von echt gebrochenrationalen Funktionen. Hier stehen einige Beispiele und Arten dazu. => Ganzen Artikel lesen …
Hebel
Physik
Als Hebel bezeichnet man einfache Maschinen, mit denen man benötigte Kräfte verringern und Hebewege dabei gleichzeitig vergrößern kann. Man unterscheidet einseitige und zweiseitige Hebel. => Ganzen Artikel lesen …
… in der Mathematik => Hyperreelle Zahl
… Graph von 1/x, siehe unter => Normalhyperbel
… Graph von 1/x, siehe unter => Normalhyperbel
… Graph von 1/x, siehe unter => Normalhyperbel
… Graph von 1/x, siehe unter => Normalhyperbel
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… Graph von 1/x, siehe unter => Normalhyperbel
… also einer Funktion wie f(x)=1/x, siehe unter => Normalhyperbel
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
… z. B. f(x)=a/Siehe unter => Hyperbel dritter Ordnung
Hyperbel dritter Ordnung
Graph
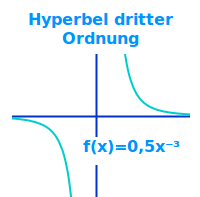
Graph einer Potenzfunktion der Form f(x)=ax^(-3). Die Funktionsgleichung f(x)=ax^(-3) kann auch geschrieben werden als f(x)=a/x³. Lies mehr unter => Hyperbeln n-ter Ordnung
… z. B. f(x)=a/x, siehe unter => Hyperbel erster Ordnung
Hyperbel erster Ordnung
Graph
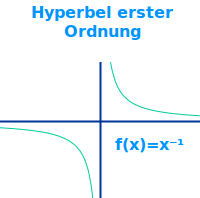
Der Graph einer Funktion mit dem Bauplan f(x) = ax^(-1) kann auch geschrieben werden als f(x)=a/x. Eine Hyperbel erster Ordnung nennt man oft kurz auch nur => Hyperbel
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
… Graph von 1/x, siehe unter => Normalhyperbel
… Graph einer Potenzfunktion der Form f(x)=ax^(-4) => Graphen von Potenzfunktionen
… z. B. f(x)=a/Siehe unter => Hypebel zweiter Ordnung
Hyperbel zweiter Ordnung
Graph
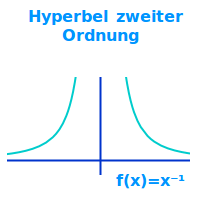
Der Graph einer Potenzfunktion der Form f(x)=ax^(-2), kann auch geschrieben werden als f(x)=a/x². Siehe unter => Hyperbeln n-ter Ordnung
Definition
Als Hyperbelfunktion bezeichnet man eine Funktion aus einer Liste von speziellen trigonometrischen Funktionen. Hyperbelfunktionen gehören damit nicht automatisch zu einer Hyperbel als Graph (diese nennen wir hie Kehrwertfunktionen). Lies mehr unter => Hyperbelfunktionen
Problem
Hyperbeln sind die Graphen von echt gebrochenrationalen Funktionen. Diese Funktionen nennt man aber nicht auch Hyperbelfunktionen. Als Hyperbelfunktionen bezeichnet man eine besondere Art trigonometrischer Funktionen. Hyperbel als Bezeichnung von Graphen und Funktionen hat damit eine uneinheitliche Bedeutung. Siehe auch => Hyperbelfunktionen
Liste
Die Hyperbelfunktionen gehören nicht zur klassischen Hyperbel f(x)=1/x. Sie bezeichnen andere Funktionstypen, die in der Schulmathematik üblicherweise aber nicht behandelt werden. Hier sind sie kurz aufgelistet. => Ganzen Artikel lesen …
… so etwas wie x hoch -3 => Hyperbeln n-ter Ordnung
Beispiele
Die Graphen von Potenzfunktion mit geradzahligen negativen Exponenten nennt man Hyperbeln. Ist der Exponent -1 spricht man kurz nur von einer Hyperbel, ist er zum Beispiel -2 spricht man von einer Hyperbel zweiter Ordnung. Dazu stehen hier kurz Beispiele. => Ganzen Artikel lesen …
… Graph von eins-durch-x, siehe => Normalhyperbel
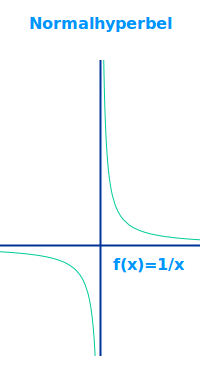
Normalhyperbel
f(x)=1/x
"Normalhyperbel" meint in Anlehnung an den Begriff der Normalparabel den Graphen der Funktion 1/x, sprich: Eins-durch-x. Der Graph ist hier mit seinen Eigenschaften kurz vorgestellt. => Ganzen Artikel lesen …
