Matrizenrechnung
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Eine solche Matrix existiert nicht für alle Verteilungen. Wenn sie aber existiert, kann sie über ein lineares Gleichungssystem berechnet werden. Das ist hier kurz skizziert. => Ganzen Artikel lesen …
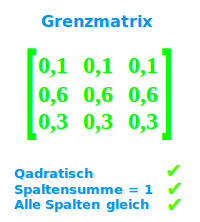Grenzmatrix
Matrizenrechnung
Wenn A die Übergangsmatrix eines Austauschprozesses ist und wenn es eine Potenz Aⁿ (A^n, meint: A hoch n) gibt, bei der kein Element der Matrix 0 ist und wenn dann alle Spalten (von oben nach unten) der Matrix identisch sind, dann ist die Matrix Aⁿ die Grenzmatrix des Austauschprozesses. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
LGS
Übersicht lineare Gleichungssysteme
LGS ist die übliche Abkürzung für ein Lineares Gleichungssystem. Ein LGS besteht aus mehreren linearen Gleichungen für die man eine einzige gemeinsame Lösung sucht. Es gibt verschiedene Arten und Lösungsverfahren, die hier kurz vorgestellt werden. => Ganzen Artikel lesen …
Es gibt dazu zwei Methoden
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Darüberhinaus ist jede Spalte der Grenzmatrix skalar proportional zum Vektor der stabilen Verteilung. Hier wird die Berechnung kurz vorgestellt. => Ganzen Artikel lesen …
… alle Spalten sind gleich, Definition unter => Grenzmatrix
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
