Exponent

2ˣ⁺¹ und 4³

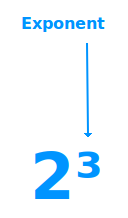
Ein Exponent ist ein Term oder auch eine einzelne Zahl, die in einer Potenz oben rechts, meist klein geschrieben steht. Bei 2ˣ⁺¹ ist das x+1 der Exponent. Bei 4³ ist die 3 der Exponent. => Ganzen Artikel lesen …

2: Exponent 0

… wie zum Beispiel 2 hoch 0, gibt fast immer 1, mehr unter => hoch Null

3: Exponent 3

… z. B. 2³Siehe unter => hoch drei

4: Exponent 4

… z. B. 2^4=Siehe unter => hoch vier

5: x Exponent

… kann verschiedene Dinge meine, siehe unter => hoch x

7: Exponent x

… kann verschiedene Dinge meine, siehe unter => hoch x

8: , im Wurzelexponenten

… z. B. 0,2te Wurzel von 3, siehe unter => r-te Wurzel

9: 0 als Wurzelexponent

… ist nicht definiert, mehr unter => nullte Wurzel

10: A-normaler Wurzelexponent

… etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel

11: Ableitung der einfachen Exponentialfunktion

… a^x abgeleitet gibt a^x·ln(a), allgemeiner unter => Exponentialfunktion ableiten

12: Abnormaler Wurzelexponent

… etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel

13: Allgemeine Exponential Gleichung

… siehe unter => Allgemeine Exponentialgleichung

14:

16: Anormale Wurzelexponenten

… etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel

17: Basis mit Bruch als Exponent

… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent

18: Basis mit rationalem Exponenten

… so etwas wie 4^(3/Siehe unter => Gebrochener Exponent

19: Beliebige Wurzelexponenten

… wie etwa die 0,2te Wurzel aus 2 => r-te Wurzel

20: Beliebiger Wurzelexponent

… wie etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel

21: Bruch-Exponenten

… wie z. B. 4^(3/4) => gebrochener Exponent

22: Bruch Exponent 0 komma 5

…zel aus 9/16 gibt 3/4, Erklärung unter => Brüche radizieren

23: Bruch Exponent 2

…4)² gibt 9/16, Erklärung unter => Brüche quadrieren

24: Bruch Exponent ein halb

…zel aus 9/16 gibt 3/4, Erklärung unter => Brüche radizieren

25: Bruch Exponent zwei

…4)² gibt 9/16, Erklärung unter => Brüche quadrieren

26: Bruch in Klammern mit Exponent

… (2/5)³, siehe unter => Brüche potenzieren

27: Bruch mit Exponent

… Bruch, der mehrmals in einer Malkette steht, siehe unter => Brüche potenzieren

28: Bruch mit Exponent 3

… Bruch, der dreimal in einer Malkette steht, siehe unter => Brüche potenzieren

29: Bruch mit Exponent 4

… Bruch, der dreimal in einer Malkette steht, siehe unter => Brüche potenzieren

30: Bruch mit Exponent drei

… Bruch, der dreimal in einer Malkette steht, siehe unter => Brüche potenzieren

31: Bruch mit Exponent ein halb

… Wurzel aus 9/16 gibt 3/4, Erklärung unter => Brüche radizieren

32: Bruch mit Exponent vier

… Bruch, der dreimal in einer Malkette steht, siehe unter => Brüche potenzieren

33: Bruch mit Exponent zwei

… (3/4)² gibt 9/16, Erklärung unter => Brüche quadrieren

34: Bruchwurzelexponent

… wie etwa die 0,2te Wurzel aus 2 => r-te Wurzel

35: Bruchzahl als Wurzelexponent

… z. B. 0,2te Wurzel von 3, siehe unter => r-te Wurzel