Durchmesser
Geometrie
Ein Durchmesser ist eine gerade Strecke, die vom Rand einer Figur, durch die Mitte bis zum gegenüberliegenden Rand geht. Von einem Durchmesser spricht man nur bei rundlichen Figuren (Kreise, Kugeln, Ellipsen etc.). Die übliche Abkürzung ist ein großes D, ein kleines d oder das Durchmesserzeichen ⌀. => Ganzen Artikel lesen …
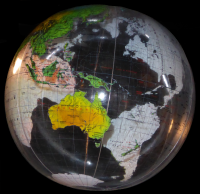Erddurchmesser
12756 km
Die Erde ist als Planet im Sonnensystem eher klein. Ihr Durchmesser ist zwar in etwa das Zweieinhalbfache des Durchmessers des Merkurs (kleinster Planet). Um aber den Durchmesser des größten Planeten, des Jupiters, zu ergeben, müsste man die Erde gut elfmal nebeneinander legen. => Ganzen Artikel lesen …
12714 km
Zwölftausendsiebenhundertundvierzehn Kilometer: der Durchmesser des Planeten Erde vom Nordpol durch die Erdmitte bis zum Südpol beträgt rund 12714 km. Das ist etwas weniger als der Durchmesser von Äquator zu Äquator. Siehe dazu => Äquatordurchmesser
Definition
Atome haben nicht zuverlässig eine Kugelform. Der Durchmesser ist dann oft definiert über die Abstände von Atomkern zu Atomkern in einem Kristall. Mehr dazu unter => Atomradius
3476 Kilometer
3476 als Durchmesser: der Mond ist deutlich kleiner als die Erde. Sein Durchmesser hat nur etwa ein Viertel bis ein Drittel des Durchmessers der Erde. Noch genauer ist der Anteil drei Elftel. Damit ist der Mond aber immerhin ein kleines Bißchen größer als der Zwergplanet Pluto. Für weitere Vergleiche, siehe unter => Planetendurchmesser
12756 km
Zwölftausendsiebenhundertundsechsundfünfzig Kilometer: der Durchmesser des Planeten Erde vom Äquator, durch die Mitte bis wieder zum Äquator ist rund 12756 Kilometer. Da die Erde zum Äquator hin etwas nach außen geschleudert ist, ist der Äquatordurchmesser etwas größer als der sogenannte Poldurchmesser. Für ein Gesamtbild, siehe unter => Erddurchmesser
Granulometrie
Der Äquivalentdurchmesser der sogenannten Granulometrie [1] ist ein "fiktiver Durchmesser" für die Körner eines Sediments. Da die Körner eines Sediments, etwa Sandkörner häufig sehr unregelmäßig geformt ist, gibt es mehrere Möglichkeiten eindeutigen Durchmesser zu definieren. => Ganzen Artikel lesen …
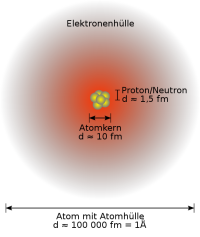Atomkerndurchmesser
Oft: 10^(-15) bis 10^(-14) Meter
- 10 hoch -15 Meter nennt man einen Femtometer. 10 hoch -14 ist entspricht dann 10 Femtometern. In dieser Größenordnung liegen die Durchmesser der Atomkerne. => Ganzen Artikel lesen …
Außendurchmesser
Vom äußeren Rand, durch die Mitte bis wieder zum äußeren Rand
Der Außendurchmesser wird oft mit einem großen D abgekürzt (Innendurchmesser oft mit d). Der Außendurchmesser geht immer vom äußeren Rand eines kreisförmigen oder kugeligen Gebildes in gerader Linie durch die Mitte bis wieder zum äußeren Rand auf der gegenüberliegenden Seite. => Ganzen Artikel lesen …
Außendurchmesser messen
Tipp
Bei Kreisen, deren Rand selbst eine deutliche Dicke hat, unterscheidet man zwei Arten von Durchmessern: den Außen- und den Außendurchmesser. Das ist zum Beispiel bei Rohren der Fall. Beide Durchmesser kann man gut mit einem Messschieber messen. Siehe auch => Messschieber
Berechnung
Ein Ball hat normalerweise Kugelform. Der Durchmesser einer Kugel geht von der Kugeloberfläche durch die Kugelmitte bis - auf der anderen - Seite wieder auf die Kugeloberfläche. Da ein Ball eine Hülle hat und diese Hülle eine Dicke hat, kann man einen Innen- und Außendurchmesser unterscheiden. Lies mehr dazu unter => Kugeldurchmesser
… um die 10 hoch -14 Meter, mehr unter => Atomkerndurchmesser
… um die 10 hoch -14 Meter, mehr unter => Atomkerndurchmesser
Anleitung
d = Durchmesser gibt es für Kreise und Kugeln. Körper wie Zylinder oder Kegel haben als Grundfläche eine Kreis. Ist der Flächeninhalt der Grundfläche bekannt, kann man daraus den Durchmesser berechnen. Eine Anleitung dazu steht unter => Kreisdurchmesser aus Kreisfläche
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
… zum Berechnen => Kugeldurchmesser
… Linie einmal quer durch das Quadrat, heißt richtig => Quadratdiagonale
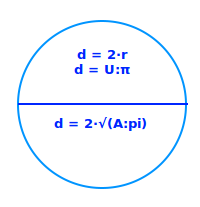Durchmesser berechnen
Übersicht
Das Wort Durchmesser bezieht sich nur auf Kreise und Kugel. Der Durchmesser d ist immer doppelt so groß wie der Radius r. Bei eckigen Figuren spricht man von einer Diagonalen, bei Ellipsen von Achsen. Hier geht es nur um Kreise und Kugeln => Ganzen Artikel lesen …
… d = U:Siehe unter => Kreisdurchmesser aus Kreisumfang
Durchmesser bestimmen
Praktisch
Man kann einen Durchmesser praktisch durch eine Messung bestimmen oder ihn aus anderen Angaben berechnen. Hier wird kurz angedeutet, wie man ihn messen kann. => Ganzen Artikel lesen …
12714 bzw. 12756 km
Von Pol zu Pol misst der Erddurchmesser 12714 km, am Äquator rund 12756 km. Lies mehr dazu unter => Erddurchmesser
… etwa 1,4 Millionen Kilometer, mehr unter => Sonnendurchmesser
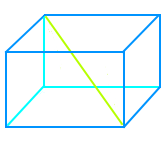Durchmesser einer Kiste
… Heißt in der Mathematik => Kistendiagonale
Von einem Durchmesser spricht man in der Geometrie bei rundlichen Figuren und Körpern. Bei eckigen Gebilden hingegen spricht man von einer Diagonalen (wörtlich: von Ecke zu Ecke). Deshalb siehe unter => Kistendiagonale
… vom Rand durch die Mitte zu Rand, mehr unter => Kugeldurchmesser
… konkrete Zahlen unter => Pizzadurchmesser
… vom Rand durch die Mitte zu Rand, mehr unter => Kreisdurchmesser
… pi mal d² durch 4, mehr unter => Kreisfläche aus Kreisdurchmesser
… U = pi mal d, mehr unter => Kreisumfang aus Kreisdurchmesser
… heißt in der Mathematik => hoch 2diagonale
… heißt in der Mathematik => hoch zweidiagonale
… heißt in der Mathematik => Kistendiagonale
… vom Rand durch die Mitte zum Rand, siehe unter => Kreisdurchmesser
… um die 10 hoch -14 Meter, mehr unter => Atomkerndurchmesser
… konkrete Zahlen unter => Pizzadurchmesser
