Distributivgesetz
Bedeutung
a·(b+c) = a·b + a·c: das Distributivgesetz aus der Schulmathematik gibt an, wie man eine Klammer auflöst, wenn in der Klammer eine Plusaufgabe oder eine Minusaufgabe steht und die ganze Klammer mal oder geteilt gerechnet wird. In der höheren Mathematik bezieht sich das Distributivgesetz auch noch auf andere Rechenarten. => Ganzen Artikel lesen …
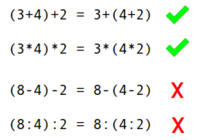Assoziativgesetz
Plus- und Mal: Klammern sind egal
Das Assoziativgesetzt besagt, dass man bei reinen Plus- und reinen Malaufgaben (Summen, Produkte) Klammern setzen kann wie man will und dass sich dadurch das Rechenergebnis niemals verändern wird. Bei der Subtraktion und Division hingegen kann sich das Ergebnis durch Setzen von Klammern verändern. => Ganzen Artikel lesen …
… gehorcht, also passt zum => Distributivgesetz
… a·(b+c) = a·b + a·c => Distributivgesetz
… (a+b)·c = a·c + b·c => Distributivgesetz
