 Cosinus
Cosinus
Definition
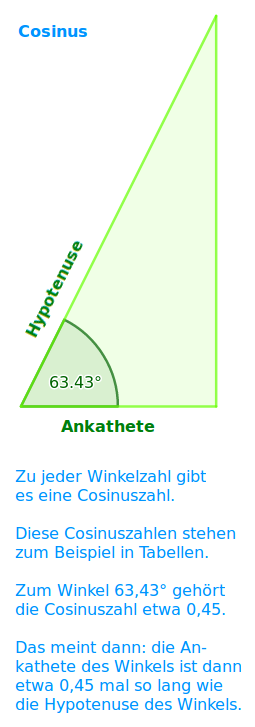
Ankathete durch Hypotenuse: der Cosinus im engeren Sinn gehört immer zu einem festen Winkel in einem rechtwinkligen Dreieck. Zu jeder möglichen Winkelzahl (0 bis 90) gibt es einen dazugehörigen Cosinuswert. Man liest ihn zum Beispiel aus einer Tabelle ab. Der Wert liegt immer zwischen 0 und 1 und sagt, wie viel mal so lang die Ankathete des Winkels ist, wie die Hypotenuse. => Ganzen Artikel lesen …
… kann mit C oder K geschrieben, werden, siehe => Cosinus
Begriffsklärung
In der Mathematik ist ein Conus ein kegelartiger Körper. In der Biologie bezeichnet das Wort eine bestimmte Art von Sehzellen. => Ganzen Artikel lesen …
… Genau 1, siehe auch => Cosinustabelle Grad
… laut Duden eine erlaubte Mehrzahl von => Cosinus
… Etwa 0.999847, siehe auch => Cosinustabelle Grad
ist: -sin(x)
 Ankathete über Cosinus
Ankathete über Cosinus
Berechnung
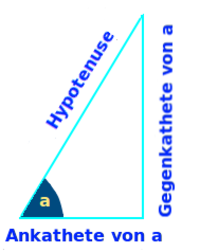
Man hat ein rechtwinkliges Dreieck. Einer der beiden nicht-90°-Grad-Winkel ist bekannt. Die kürzere der zwei Seiten direkt an diesem Winkel ist die sogenannte Ankathete. Sie berührt immer den Winkel. Es wird gezeigt, wie man ihre Länge berechnet. => Ganzen Artikel lesen …
Winkel
Der Arkuscosinus, auch cos-hoch-minus-eins, gibt an, welcher Winkel zu einem Cosinuswert gehört: man hat den Cosinuswert eines Winkels gegeben. Man will nun wissen, welcher Winkel diesen Cosinus hat. Die Funktion Arkuscosinus gibt genau diesen Winkel zurück. => Ganzen Artikel lesen …
… gibt sin(Siehe unter => cosinus x aufgeleitet
… gibt sin(Siehe unter => cosinus x aufgeleitet
… gibt sin(Siehe unter => cosinus x aufgeleitet
… gibt sin(Siehe unter => cosinus x aufgeleitet
Vektorrechnung
Als Cosinus-Ähnlichkeit bezeichnet man einen Zahlenwert zwischen -1 und 1, der für die Ähnlichkeit von zwei Wortfolgen steht. Je ähnlicher sich zwei Wortfolgen, etwa Sätze, sind desto näher liegt der Wert bei 1. Mit Hilfe der Vektorrechnung läßt sich die Ähnlichkeit recht unkompliziert berechnen. Das ist hier mit einem Beispiel vorgestellt. => Ganzen Artikel lesen …
… Genau 0, siehe auch => Cosinustabelle Grad
… Genau 0, siehe auch => Cosinustabelle Grad
… Genau 1, siehe auch => Cosinustabelle Grad
… Etwa 0.707106, siehe auch => Cosinustabelle Grad
… Genau 0, siehe auch => Cosinustabelle Grad
… cos(x) abgeleitet gibt -sin(x). Siehe auch => Ableitungen [Beispiele]
… gibt -sin(x) => Ableitungen [Beispiele]
… gibt Sinus, mehr unter => Cosinus x aufgeleitet
… gibt sin(x), siehe auch => Aufleitungsregeln
… gibt sin(Siehe unter => cosinus x aufgeleitet
Methoden
Außer der Formel cos(a) = AK/HY gibt es noch andere Methoden. Diese sind kurz vorgestellt auf der Seite => Cosinus bestimmen
Methoden
Der Cosinus eines Winkels sagt: wie viel mal so groß ist die Ankathete dieses Winkels wie die Hypotenuse? Es werden verschiedene Methoden vorgestellt, wie man diese Zahl berechnen kann. Was der Cosinus genau meint ist erklärt auf der Seite => Cosinus
cos(x) abgeleitet gibt -sin(x)
… für normale Gradzahlen => Cosinustabelle Grad
… für normale Gradzahlen => Cosinustabelle Grad
… für Winkel, siehe unter => Arkuscosinus
Für Winkel: Arcuscosinus
Cosinus hoch minus eins ist eine Taschenrechnerfunktion für den sogenannten Arkuscosinus, die Umkehrfunktion zum Cosinus. Hoch minus eins hat hier nicht die übliche arithemtische Bedeutung eines Kehrwertes sondern ist lediglich ein Taschenrechnerkürzel. Wenn der Cosinus von 90° genau 0 ist, dann ist der Arkuscosinus von 0 genau 90°. Lies mehr unter => Arkuscosinus
… Definition und Berechnung, siehe unter => Winkel zwischen Vektoren
… Definition und Berechnung, siehe unter => Winkel über Skalarprodukt
… Cosinustabelle im Bogenmaß, siehe unter => Cosinustabelle Rad
… Cosinustabelle im Bogenmaß, siehe unter => Cosinustabelle Rad

