Physik
Als Bahnkurve allgemein bezeichnet man eine zusammenhängende Kurve, das heißt eine Linie, die durch jene Raumpunkte gebildet wird, die ein Massenpunkt durchläuft. [1] Das klassische Beispiele sind als Massepunkte idealisierte Himmelskörper oder Geschosse in der Ballistik. Spricht man von submikroskopisch kleinen Teilchen, etwa Elektronen in einer Nebelkammer, ist auch die Bezeichnung Teilchenbahn [2] üblich. Der Bahnbegriff macht Sinn in der klassischen Physik, nicht aber in der Quantenphysik, wo er keine Bedeutung hat. [1][2][3] Kurz Bahn oder auch Trajektorie sind Überbegriffe. Siehe mehr unter => Trajektorie (Physik)
… a meint Beschleunigung, siehe unter => Beschleunigung-Zeit-Diagramm
Definition
Auf der x-Achse steht die Zeit, auf der y-Achse steht die gelernte Stofftmenge. Je steiler die Kurve, desto schneller hat man etwas gelernt. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… a meint Beschleunigung, siehe unter => Beschleunigung-Zeit-Diagramm
 Bahkauv
Bahkauv
… Phantasiefigur (Bachkalb), siehe auch => Aachen
 Backenzahnkurve
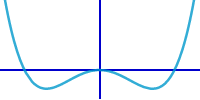
Backenzahnkurve
Graph
Graph einer Biquadratischen Funktion mit gegensinnigen Vorzeichen: die Form kann an die typische Darstellung eines Backenzahns erinnern. Graph und Funktionsgleichung sind hier kurz erläutert. => Ganzen Artikel lesen …
Bedeutungen
In der Geometrie ist eine Kurve eine zusammenhängende Linie. Sie kann gerade oder auch gebogen sein. Für Funktionen ist Kurve ein Synonym für den Graphen. Beide Bedeutungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …

