ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
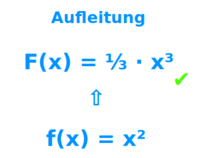
1: Aufleitung

Stammfunktion

Eine Aufleitung F(x) von einer Funktion f(x) ist dasselbe wie eine Stammfunktion von f(x). Das Wort wird häufig benutzt, um den Zusammenhang mit der entegegengesetzen Operation der Ableitung zu verdeutlichen. Lies unter => Stammfunktion
2: 0 aufleitung

… gibt 0, mehr unter => 0 aufgeleitet
3: 1 aufleitung

… gibt x, mehr unter => 1 aufgeleitet
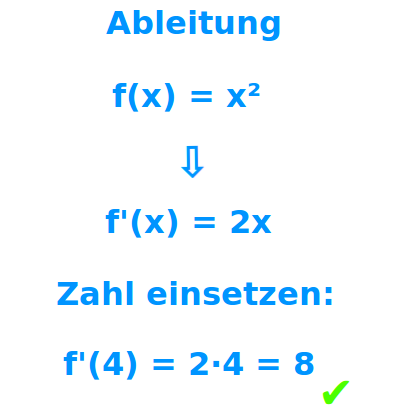4: Ableitung

f'(x)

Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
5: x aufleitung

… ist 0,5x², mehr unter => x aufgeleitet
6: C Aufleitung

… Zahl + oder - am Ende einer Aufleitung => Integrationskonstante
7: Aufleitungen

Liste für F(x)

Liste von Standardaufleitungen - Aufleitung meint hier: eine Stammfunktion F(x) einer gegebenen Funktion f(x). Aufleitungen häufig gesuchter Funktionen nennt man oft auch Stammintegrale. Hier steht eine Übersicht häufiger und wichtiger Stammintegrale. => Ganzen Artikel lesen …
8: Aufleitung 0

… gibt 0, mehr unter => 0 aufgeleitet
9: Aufleitung 0 Aufleitung von 0

… gibt 0, mehr unter => 0 aufgeleitet
10: Aufleitung 1

… gibt x, mehr unter => 1 aufgeleitet
11: Aufleitung 1 Aufleitung von 1

… gibt x, mehr unter => 1 aufgeleitet
12: Aufleitung C

… Zahl + oder - am Ende einer Aufleitung => Integrationskonstante
13: Aufleitung cosinus Aufleitung von cosinus

… gibt sin(Siehe unter => cosinus x aufgeleitet
14: Aufleitung cosinus x

… gibt sin(Siehe unter => cosinus x aufgeleitet
15: Aufleitung der einfachen ln-Funktion

ln(x) aufgeleitet gibt: x·ln(x)+x
16: Aufleitung der natürlichen Logarithmusfunktion

ln(x) aufgeleitet gibt: x·ln(x)+x
17: Aufleitung e hoch Aufleitung von e hoch

… ist e hoch x, mehr unter => e hoch x aufgeleitet
18: Aufleitung e hoch x

… ist e hoch x, mehr unter => e hoch x aufgeleitet
19: Aufleitung Eins

… gibt x, mehr unter => 1 aufgeleitet
20: Aufleitung Eins Aufleitung von Eins

… gibt x, mehr unter => 1 aufgeleitet
21: Aufleitung mit C

… Zahl + oder - am Ende einer Aufleitung => Integrationskonstante
22: Aufleitung mit u und v

… Erklärung mit Beispiel unter => Partiell integrieren
23: Aufleitung mit v und u

… Erklärung mit Beispiel unter => Partiell integrieren
24: Aufleitung Null

… gibt 0, mehr unter => 0 aufgeleitet
25: Aufleitung Null Aufleitung von Null

… gibt 0, mehr unter => 0 aufgeleitet
26: Aufleitung sinus Aufleitung von sinus

… -cos(Siehe unter => sinus x aufgeleitet
27: Aufleitung sinus x

… -cos(Siehe unter => sinus x aufgeleitet
28: Aufleitung unbekannt

F(x) noch unbekannt

Die Aufleitung einer Funktion f(x) ist die Stammfunktion F(x) finden. Ist die Stammfunktion unbekannt, sagt man auch, dass f(x) nicht aufleitbar. Mehr dazu unter => nicht aufleitbar
29: Aufleitung von 6

… ist 6x, mehr dazu unter => 6 aufleiten
30: Aufleitung von einer Cosinuskurve

… gibt sin(Siehe unter => cosinus x aufgeleitet
31: Aufleitung von einer e hoch x

… ist e hoch x, mehr unter => e hoch x aufgeleitet
32: Aufleitung von einer Sinuskurve

… -cos(Siehe unter => sinus x aufgeleitet
33: Aufleitung von einer Tangenskurve

… gibt 0, mehr unter => 0 aufgeleitet
34: Aufleitung von einer Wurzel

… (2/3)x^1,5, mehr unter => Wurzel aufgeleitet
35: Aufleitung von einer Zahl

… ist immer Zahl mal x, mehr unter => Zahl aufgeleitet
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023