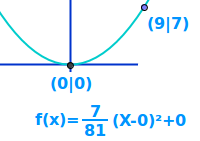
Scheitelpunktform aus zwei Punkten
20 Aufgaben mit Lösungen
Gegeben sind zwei Punkte S und P. Der Punkt S ist immer der Scheitelpunkt eine Parabel. Finde die Gleichung der Parabel durch die Punkte S und P in der Scheitelpunktform f(x)=a(x-d)²+e. Mache zu jeder Aufgabe eine grobe (nicht maßstäbliche) Skizze, die zeigt, wo in etwa im Koordinatensystem die Punkte liegen.
a) S(2|1) P(5|10)
c) S(2|1) P(5|73)
d) S(4|3) P(8|-29)
e) S(4|3) P(0|2)
f) S(100|200) P(101|201)
g) S(100|200) P(101|209)
h) S(100|200) P(104|280)
i) S(820|899) P(824|979)
j) S(820|899) P(818|891)
Wahr oder falsch?
k) Der Scheitelpunkt ist immer der tiefste Punkt einer Parabel.
l) Der f(x)-Wert eines Punktes [dasselbe wie y] ist immer größer als der x-Wert.
m) Alle Parabeln aus den Aufgaben a bis j sind nach oben geöffnet.
n) Alle Parabeln aus den Aufaben a bis j sind nach unten geöffnet.
o) Nicht alle Parabeln aus den Aufgaben a bis j sind nach unten geöffnet.
Lückentexte
p) Das a in der Gleichung ist der sogenannte ____________________.
q) Das d in der Gleichung ist der _______________ des Scheitelpunktes.
r) Ein positiver Streckungsfaktor bedeutet, dass die Parabel nach oben ______________ geöffnet ist.
s) Die Scheitelpunktform ist eine von mehreren möglichen ________________________.
t) SPF ist eine gängige Abkürzung für die ____________________________ von Parabeln.
Lösungen
a) f(x) = 1(x-2)² + 1
b) f(x) = 2(x-2)² + 1
c) f(x) = 8(x-2)² + 1
d) f(x) = -2(x-4)² + 3
e) f(x) = -0,0625(x-4)²+3
f) f(x) = 1(x-100)²+200
g) f(x) = 9(x-100)²+200
h) f(x) = 5(x-100)²+200
i) f(x) = 5(x-820)²+899
j) f(x) = -2(x-820)²+899
k) Falsch
l) Falsch
m) Falsch
n) Falsch
o) Falsch
p) Streckungsfaktor
q) x-Wert
r) geöffnet
s) Parabelgleichungen
t) Scheitelpunktform