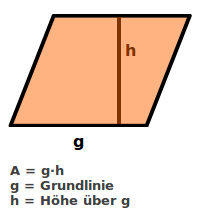
Parallelogrammfläche berechnen
10 Verständnisfragen für den Einstieg
a) Eine Seite eines Parallelogramms sei 10cm lang. Die dazugehörige Höhe habe die Länge 4cm. Wie groß ist der Flächeninhalt des Parallelogramms?
b) Die Höhe eines Parallelogramms sei das Dreifache der Länge seiner Grundseite. Was ist der Flächeninhalt des Parallelogramms, wenn die Länge seiner Grundseite 4cm ist?
c) Die Länge der Grundseite sei ein halber Meter, die dazugehörige Höhe sei ein Viertel Meter. Was ist der Flächeninhalt des Parallelogramms?
d) Der Flächeninhalt eines Parallelogramms sei 100 Quadratzentimeter. Wie hoch ist das Parallelogramm über der Grundseite g, wenn g eine Länge von 20 Zentimetern hat?
e) Der Flächeninhalt eines Parallelogramms sei 100 Quadratzentimeter. Wie hoch ist das Parallelogramm über der Grundseite g, wenn g eine Länge von einem halben Zentimeter hat?
Wahr oder falsch?
f) Eine Formel für den Flächeninhalt eines Trapezes gilt automatisch auch für den Flächeninhalt eines Parallelogramms. Das muss so sein, da ja jedes Parallelogramm immer auch ein Trapez ist.
g) Die Aussage in f ist falsch, da es auch Parallelogramme gibt, die kein Trapez sind.
h) Wenn ich bei einem Parallelogramm die Grundseite unverändert immer gleich lang lassse aber die Höhe verdreifache, dann verdreifacht sich auch der Flächeninhalt.
i) Haben ein Parallelogramm und ein Dreieck die gleiche Grundseite und die gleiche Höhe, dann haben sie auch den gleichen Flächeninhalt.
j) Es gibt Parallelogramme die den gleichen Flächeninhalt haben wie irgendein Quadrat.
Lösungen
a) 40 Quadratzentimeter
b) 48 Quadratzentimeter
c) Ein Achtel Quadratmeter
d) 5 Zentimeter
e) 2 Meter
f) wahr
g) falsch
h) wahr
i) falsch
j) wahr