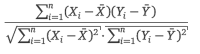Korrelationskoeffizient nach Pearson
Bedeutung | Beispiele
© 2016
- 2025
Basiswissen ·
Synonyme ·
Bedeutung ·
Werte von 0 bis 1 ·
Wert gleich 0 ·
Division durch 0 ·
Sonstiges
Basiswissen
Gibt an, wie gut zwei Größen sich mit je-desto Sätzen in ihrer Veränderung beschreiben lassen: Je mehr Dünger desto mehr Pflanzenertrag: wie gut dieser Satz gilt, kann für bestimmte Datensätze als Zahlenwert von -1 bis 1 angegeben werden.
Synonyme
- Der Korrelationskoeffizient ist ein Zusammenhangsmaß ↗
- Der Korrelationskoeffizient nach Pearson heißt oft auch einfach nur ...
- Korrelationskoeffizient oder auch Korrelationskoeffizient nach Bravais.
- Ein häufige Abkürzung ist das kleine r.
Bedeutung
- Er sagt, wie gut sich die zusammengehörigen Werte zweier Variablen mit ...
- je-desto-Sätzen und in linearen Abhängigkeiten ausdrücken lassen.
- Die Werte liegen immer zwischen -1 und 1:
Werte von 0 bis 1
- Positive Korrelation: Je größer das eine, desto größer auch das andere.
- Beispiel: Je größer ein Mensch, desto größer ist auch seine Schuhgröße.
- Je näher der Wert bei 1 ist, desto linearer ist auch der Zusammenhang
- Die Steigung ist dann positiv.
Werte von -1 bis 0
- Je größer das eine, desto kleiner das andere.
- Beispiel: Je höher die Temperatur in einem Skigebiet, ...
- desto kleiner die Anzahl der Urlaubsgäste.
- Je näher an der Wert bei -1 ist, desto linearer ist der Zusammenhang ...
- aber mit negativer Steigung.
Wert gleich 0
- Keine Korrelation, unkorreliert: das eine hat nichts mit dem anderen zu tun.
- Beispiel: Die Größe der Hausnummer mit der durchschnittlichen
- Körpergröße der Bewohner dieses Hauses.
- Je näher der Koeffizient an der Null liegt, desto ...
- weniger linear ist der Zusammenhang.
Division durch 0
Liegen die Punkte auf einer horizontalen Geraden parallel zur x-Achse, dann ist der Korrelationskoeffizient nach Pearson nicht definiert. Anschaulich würde das heißen: Egal wie groß x ist, y hat immer den gleichen Wert. In den Berechnungsformeln tritt dann an irgendeiner Stelle eine Division durch 0 auf. Daran merkt man, dass dieser Fall nicht definiert ist. Analog gilt das gleiche für Punkte die auf einer senkrechten Geraden liegen (parallel zur y-Achse). Auch hier führt die Formel zu einer Division durch 0, der Korrelationskoeffizient ist also nicht definiert.
Sonstiges
- Der Zähler in der Formel ist die Kovarianz der Daten.
- Die Wurzelterme im Nenner sind die Standardabweichungen.
- Dieser Koeffizient ist standardisiert (festes Ergebnisintervall).