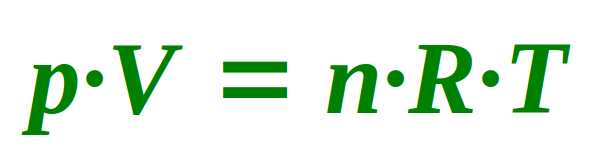Ideales Gasgesetz
Chemie
Basiswissen
pV = nRT: dieses Gesetz gilt für ein ideales Gas. Luft bei Umgebungstemperatur und normalem Druck ist ein typisches Beispiel für ein annähernd ideales Gas. Das ist hier näher erklärt.
Formel für das ideale Gasgesetz
- pV = nRT
Legende
- p = Druck des Gases, z. B. Pascal ↗
- V = Volumen des Gases, z. B. in Kubikmeter[n] ↗
- n = Stoffmenge, z. B. in Mol ↗
- T = Temperatur in Kelvin ↗
Allgemeine Gaskonstante
- R hat den Wert 8,314598 J pro Kelvin und mol
- Siehe auch allgemeine Gaskonstante ↗
Was ist ein ideales Gas?
Man denkt sich Gase als eine Ansammlung sehr vieler kleiner Teilchen, den Gasmolekülen. Die Teilchen haben in der Wirklichkeit eine Größe und zwischen ihnen wirken auch Anziehungskräfte. Das macht Formeln zur Berechnung solcher Gase sehr schwer handhabbar. Stellt man sich aber diese Teilchen so vor, als hätten sie zwar eine Masse aber kein eigenes Volumen und stellt man sich weiter vor, als gäbe es zwischen ihnen keine Anziehungs- oder Abstoßungskräfte, dann erhält man damit sehr viel besser handhabbare Formeln, ohne dass dabei zwangsläufig große Fehler auftreten. Lies mehr dazu unter ideales Gas ↗
Wann gilt das ideale Gasgesetz nicht?
Sind die Gasteilchen sehr eng beieinander, dann spielt ihre eigene Ausdehnung eine immer größere Rolle. Diese Tatsache macht mit wachsendem Anteil des Teilchenvolumens am gesamten Volumen den Rechenfehler des idealen Gasgesetzes immer größerer. Der Fall tritt zum Beispiel bei hohen Drücken auf. Man verwendet dann die Formel für reales Gasgesetz ↗
Fußnoten
- [1] Johannes Diderik van der Waals: Over de Continuiteit van den gas- en vloeistoftoestand. Sijthoff, Leiden 1873, deutsch: Die Kontinuität des gasförmigen und flüssigen Zustandes. Barth, Leipzig 1881
- [2] James Clerk Maxwell: On The dynamical evidence of the moleculkar constitution of bodies. In: Nature. Band 11, 1875, S. 357–359 und 374–377
