Totale Ableitung
Größte Steigung
Die totale Ableitung, oft auch totales Differential oder Gradient genannt gibt die maximale Steigung einer mehdimenensionalen Funktion von einem Punkt aus gesehen an als Richtung (wohin) und als Wert (wie stark) an. Die totale Ableitung wird hier weiter betracht im Artikel => Gradient eines Skalarfeldes
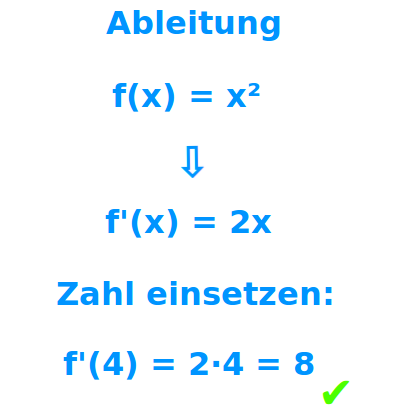
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
… die noch gar nicht abgeleitete Funktion, mehr unter => eigentliche Funktion
… also f'Siehe unter => dritte Ableitung
… f''(x) oder partielle Ableitung, siehe unter => Doppelte Ableitung
… gibt immer 0, mehr unter => Zahl ableiten
