Inverse Matrix berechnen
Verschiedene Verfahren dazu
Eine Matrix kann nur invertiert werden, wenn sie quadratisch ist (genauso viele Spalten wie Zeilen) und wenn sie reguläre ist (die Determinante ist nicht gleich 0). Die Inverse Matrix A⁻¹ kann dann mit verschiedenen Verfahren bestimmt werden. => Ganzen Artikel lesen …
Matrizenrechnung
In der Rechnung mit Matrizen steht „die Inverse“ oft als Kurzform für eine sogenannte => Inverse Matrix [1]
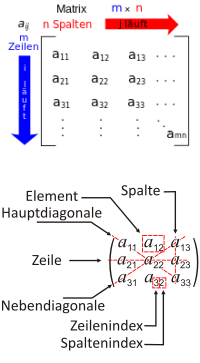Matrix
Mathematik
Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen [1], so als sei die ganze Matrix eine Zahl. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… Anleitung unter => inverse Matrix berechnen
… Anleitung unter => inverse Matrix berechnen
Es gibt dazu zwei Methoden
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Darüberhinaus ist jede Spalte der Grenzmatrix skalar proportional zum Vektor der stabilen Verteilung. Hier wird die Berechnung kurz vorgestellt. => Ganzen Artikel lesen …
… Anleitung unter => inverse Matrix berechnen
… Anleitung unter => inverse Matrix berechnen
