Analysis
Die erste Ableitung f'(x) einer Funktion f(x) kann man sowohl rein anschaulich nur grapisch erstellen. Zum anderen aber kann man die erste Ableitung auch anschaulich deuten, also interpretieren. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Ganz am Anfang
In der Zahl 320 ist die erste Ziffer eine 3. „Die erste“ gibt hier die Position innerhalb einer Rangfolge an. Sie hat damit mathematisch gesehen die Rolle einer => Ordinalzahl
 Ableitung
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
 Anschaulich
Anschaulich
Mit einem Denkbild
So, dass visuell-grapisches Denken mit einbezogen wird. Beispiel: was gibt 4 geteilt durch 0,5? Man kann die Aufgabe formal-rechnerisch, indem man sie z. B. als Bruch schreibt 4/0,5 dann erweitert 40/5 und am Ende den Wert berechnet, hier also 8. Als Alternative zur formalen Lösung wird hier ein anschaulicher Weg gezeigt. Lies mehr unter => anschaulich rechnen
… f'(x) skizzieren und auch deuten können => erste Ableitung anschaulich
… Bedeutungen unter => erste Ableitung gleich null
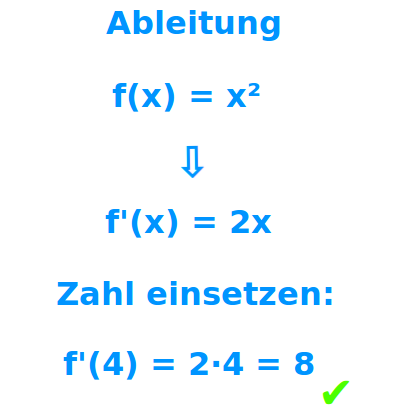
… wie x² zu Siehe unter => erste Ableitung bilden
… Bedeutungen unter => erste Ableitung gleich null
… siehe unter => Erste Ableitung bilden

