Anleitung
O = 2·Pi·r² + 2·Pi·r·h ist die Grundformel zur Berechnung der Zylinderoberfläche. Das Ergebnis kann man zum Beispiel in Quadratzentimetern oder Quadratmetern angeben. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Zylinderoberfläche
Definition
Die Oberfläche O eines Zylinders setzt sich aus drei Teilflächen zusammen: der Grundfläche G, der Deckfläche D und der Mantelfläche M. Die Grund- und Deckfläche sind beide gleich groß. Die Grundformel für die Berechnung der Zylinder oberfläche ist O = 2·Pi·r² + 2·Pi·r·h. Mehr dazu unter => Zylinderoberfläche berechnen
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… zum Beispiel in cm², siehe unter => Quaderoberfläche
… zum Beispiel in cm², siehe unter => Zylinderoberfläche
Grundidee
Eine Oberfläche O wird angegeben in Einheiten wie Quadratkilometer [km²], Quadratmeter [m²] oder bei sehr kleinen Körpern auch in Quadratzentimetern [cm²]. Zur Berechnung benutzt sogenannte => Oberflächenformeln
… zum Beispiel in cm², siehe unter => Pyramidenoberfläche
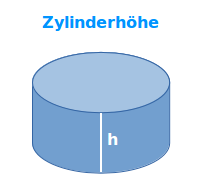Zylinderhoehe berechnen
Formeln zur Berechnung der Zylinderhöhe h
Die Höhe eines Zylinders ist der kürzeste Abstand zwischen seiner Grund- und Deckfläche. Je nachdem was gegeben ist, gibt es verschiedene Möglichkeiten der Berechnung. => Ganzen Artikel lesen …
