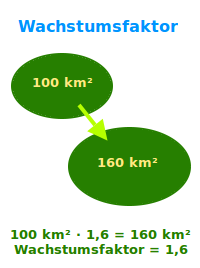
Wachstumsfaktor
Mathematik
Alter Wert · Wachstumstumsfaktor = neuer Wert: der Wachstumsfaktor gibt an, womit man einen alten Wert multiplizieren muss (Faktor), um den darauffolgenden neuen Wert zu erhalten. In einer Exponentialfunktion wie f(x) = a·b^x ist das kleine b der Wachstumsfaktor. Das ist hier näher erklärt. => Ganzen Artikel lesen …
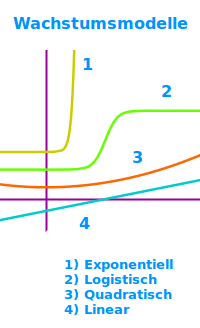Wachstumsarten
Bergriffsklärung
Positiv, negativ, linear, quadratisch oder expoentiell: man teilt verschiedene Wachstumsvorgänge zum einen danach ein, ob etwas tatsächlich wächst oder gleichbleibt oder abnimmt. Andererseits teilt man Wachstum auch nach mathematischen Funktionen ein, die es gut beschreiben. Beides wird hier kurz vorgestellt. => Ganzen Artikel lesen …
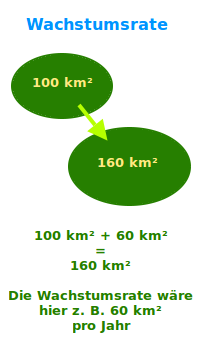Wachstumsrate
Definition
Der höchste Berg der Erde ist der Mount Everest. Er wächst jedes Jahr um einen Zentimeter in die Höhe. Eine Wachstumsrate ist ein Zuwachs, der in einem bestimmten Zeitraum stattfindet. Hier: 1 cm/Jahr. => Ganzen Artikel lesen …
Wachstumsraten
Beispiele
Eine Rate ist eine Änderung mit der Zeit. Hier stehen Zahlenbeispiele für Prozesse, bei denen etwas mit der Zeit wächst, also im mathematischen Sinne größer wird. => Ganzen Artikel lesen …
… Wachstumsfaktor ist konstant, mehr unter => Exponentielles Wachstum
… Übersicht unter => Wachstumsmodelle
Funktion
Als mathematische Funktion f(x), wie etwa linear, quadratisch oder exponentiell, siehe unter => Wachstumsmodelle
… ist typisch für ein => exponentielles Wachstum
… Erklärung und Aufgaben => Prozentsatz in Wachstumsfaktor
… Zum Beispiel 4 % aus dem Faktor 1,04 | Siehe unter => Wachstumsfaktor in Prozentsatz
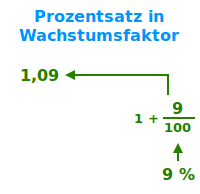Prozentsatz in Wachstumsfaktor
Umrechnung
Von 1992 bis 2017 wuchs die Verkehrsfläche in Deutschland von 16441 km² auf 18046 km². Das war ein prozentualer Anstieg von etwa 9,8 % oder - als Wachstumsfaktor - 1,098. Hier wird die Umrechnung erklärt. => Ganzen Artikel lesen …
… Erklärung und Aufgaben => Prozentsatz in Wachstumsfaktor => qck
… Erklärung und Aufgaben => Prozentsatz in Wachstumsfaktor => qck
… 4 % wären 1,04 ⭢ mehr unter => Prozentsatz in Wachstumsfaktor => qck
Umrechnung
b = e^(-λ) ist die Formel zur Berechnung des Wachstumsfaktors aus einer bekannten Zerfallskonstanten λ. Die Zerfallskonstante kommt vor im sogenannten Zerfallsgesetz N(t) = N₀·e^(-λ·t) während der Wachstumsfaktor in der Darstellung über die erweiterte Exponentialfunktion N(t) = N₀·b^t verwendet wird. Für die umgekehrte Rechnung siehe unter => Zerfallskonstante aus Wachstumsfaktor
Formeln
Ein Wachstum von 2 % ergibt eine Wachstumsfaktor von 1,02: dieser Wachstumsfaktor spielt unter anderem in den Naturwissenschaften, der Technik und dem Geldwesen eine Rolle. Verschiedene Berechnungsarten sind hier kurz erklärt. => Ganzen Artikel lesen …
Umrechnung
Ein Wachstumsfaktor von 1,4 ist ein Prozentsatz von 40 %. Die Umrechnung ist hier kurz erklärt. => Ganzen Artikel lesen …
… siehe unter => Wachstumsfaktor in Prozentsatz
… Erklärung und Aufgaben => Prozentsatz in Wachstumsfaktor => qck
Umrechnung
λ = -ln(b) ist die Formel zur Berechnung der Zerfallskonstanten λ aus einem bekannten Wachstumsfaktor b. Die Zerfallskonstante kommt vor im Zerfallsgesetz N(t) = N₀·e^(-λ·t) während der Wachstumsfaktor in der Darstellung über die erweiterte Exponentialfunktion N(t) = N₀·b^t verwendet wird. Für die umgekehrte Rechnung siehe unter => Wachstumsfaktor aus Zerfallskonstante
… siehe unter => Wachstumsfaktor aus Zerfallskonstante
… siehe unter => Prozentsatz aus Wachstumsfaktor
