Sinus, Cosinus und Tangens
Trigonometrie nennt man die Geometrie mit Hilfe des Sinus, Cosinus und Tangens. Die Ideen zur Trigonometrie sind ursprünglich an Dreiecken mit einem 90-Grad-Winkel innen entstanden. Von dort aus wurden sie dann auch auf andere Rechengebiete übertragen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
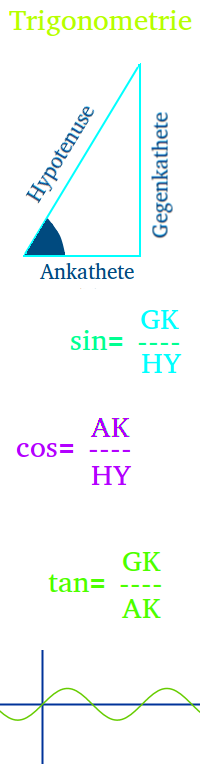Trigonometrie
Sin, cos, tan
Unter dem Überbegriff Trigonometrie werden verschiedene Verfahren zur Berechnung von Längen und Winkeln an Dreiecken zusammengefasst. Das zentrale Konzept ist der Tangens, Cosinus und Sinus. => Ganzen Artikel lesen …
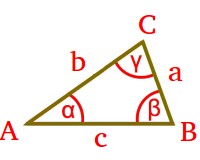Dreieck
ABC
Definition: Jede flache (2D) Figur mit genau drei Ecken und genau drei geraden Verbindungslinien zwischen den Linien ist ein Dreieck. Ein Dreieck ist damit eine Sonderfall eines Vielecks. Eine Themenübersicht steht auf der Seite => Dreiecksrechnung
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
