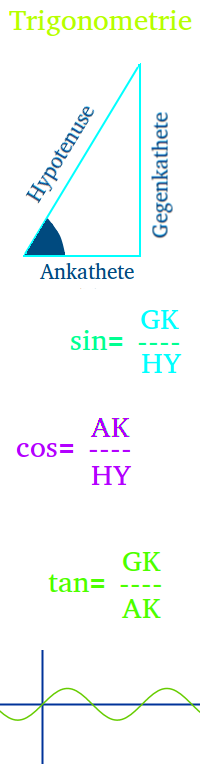Trigonometrie
Sin, cos, tan
Unter dem Überbegriff Trigonometrie werden verschiedene Verfahren zur Berechnung von Längen und Winkeln an Dreiecken zusammengefasst. Das zentrale Konzept ist der Tangens, Cosinus und Sinus. => Ganzen Artikel lesen …
… mit sin, cos und tan => Trigonometrie
… mit sin, cos und tan => Trigonometrie
… mit sin, cos und tan => Trigonometrie
… mit sin, cos und tan => Trigonometrie
… mit sin, cos und tan => Trigonometrie
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
Lösungsidee
Die Höhe h einer Pyramide ist die Strecke senkrecht von der Spitze bis zur Grundfläche. Kennt man die Länge der Pyramidenseitenkante und die Seitenlänge der Grundfläche, kann man daraus die Höhe h berechnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Anleitung
Die Diagonale teilt das Quadrat in zwei gleichschenklige Dreiecke. Jedes dieser zwei Dreiecke hat einen 90° Innenwinkel und zwei je 45° große Winkel. Die zwei kurzen Seiten a und b sind die Katheten, die lange Seite c ist die Hypotenuse. Die Hypotenuse ist auch die gesuchte Diagonale. Über die Definition des Sinus erhält man: c = a:sin(45°) oder c ≈ 1,41 mal a. Siehe auch => Definition
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… Die Trigonometrie auf der Oberfläche von Kugeln, siehe z. B. ein => sphärisches Dreieck
… siehe unter => Steigung in Steigungswinkel
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
Verständnisfragen rund um Dreiecksberechnungen
a) Die Katheten eines Dreiecks sind beide 2 Meter lang. Wie lang ist die Hypotenuse? => Ganzen Artikel lesen …
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
Sinus, Cosinus und Tangens
Trigonometrie nennt man die Geometrie mit Hilfe des Sinus, Cosinus und Tangens. Die Ideen zur Trigonometrie sind ursprünglich an Dreiecken mit einem 90-Grad-Winkel innen entstanden. Von dort aus wurden sie dann auch auf andere Rechengebiete übertragen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
… mit sin, cos und tan, siehe => Trigonometrie im rechtwinkligen Dreieck
Sammlung
Hier geht zu einer Aufgabensammlung zur Trigonometrie als Textaufgaben formuliert. Zu allen Aufgaben gibt es auch Lösungen. Hier stehen einige Tipps. => Ganzen Artikel lesen …
Aufgaben
Gemischte Fragen rund um die Dreiecksberechnung: hier stehen kurz erst einige Fachworte zur Trigonometrie. Über qck geht es dann zu Fragen zum Grundverständnis. Zu allen Fragen gibt es auch die richtige Antwort. => Ganzen Artikel lesen …
