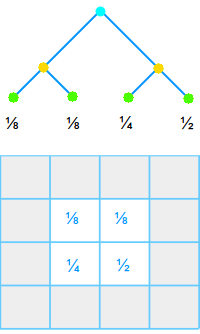
Schnittwahrscheinlichkeit
P(A∩B)
P(A∩B) wird gelesen als die Wahrscheinlichkeit von A geschnitten mit B. Sie heißt Schnittwahrscheinlichkeit, Verbundwahrscheinlichkeit oder auch gemeinsame Wahrscheinlichkeit. Sie kommt in Baumdiagrammen und Vierfeldertafeln vor. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… in der Stochastik die Wahrscheinlichkeit für ein => Elementarereignis
Baumdiagramm
Dort wo ein Baumdiagramm endet liegen die Ausgänge. Die Ausgänge sind meistens ganz unten oder ganz rechts in einem Baumdiagramm zu sehen. Die Wahrscheinlichkeiten, die zu jedem einzelnen Ausgang gehören, nennt man entsprechend Ausgangswahrscheinlichkeiten. => Ganzen Artikel lesen …
Bedingte Wahrscheinlichkeit
Definition
Die Wahrscheinlichkeit, dass jemand mit blonden Haaren blaue Augen hat ist höher, als die Warscheinlichkeit, dass jemand mit schwarzen Haaren blaue Augen hat: die Haarfarbe bedingt (beeinflusst) die Wahrscheinlichkeit für Blauäugigkeit. Die Augenfarbe Blau ist damit eine bedingte Wahrscheinlichkeit. Dieser Begriff wird in der Stochastik rechnerisch gefasst und hier kurz erklärt. => Ganzen Artikel lesen …
Wahrscheinlichkeit
Stochastik
Die Wahrscheinlichkeit ist immer eine Zahl zwischen 0 und 1. [10] Als Wahrscheinlichkeit bezeichnet man den Anteil, auch relative Häufigkeit genannt, eines Ereignisses bei vielen Wiederholungen an der Gesamtzahl der Versuche. Die Wahrscheinlichkeit „ein Sechstel“ beim Würfeln kann zum Beispiel meinen: wenn man sehr oft würfelt, dann kommt meistens in einem Sechstel der Fälle eine 6. => Ganzen Artikel lesen …
Arten
Theoretische, empirische oder bedingte Wahrscheinlichkeit: hier sind verschiedene Arten kurz vorgestellt. => Ganzen Artikel lesen …
… im Zusammenhang mit einem Hypotesentest dasselbe wie der => Fehler erster Art
