Rhombusfläche
… z. B. in cm² oder m² => Rautenfläche
Begriffsklärung
Außenfläche kann einmal die Flächen im freien Gelände meinen: „Das Fabrikgebäude muss täglich von innen gereinigt werden. Aber auch die Außenflächen sollten sauber gehalten werden.“ Bei einem geometrischen Körper kann die Außenfläche aber auch die nach außen weisende Fläche eines Hohlkörpers meinen. Diese nennt man oft auch die => Oberfläche
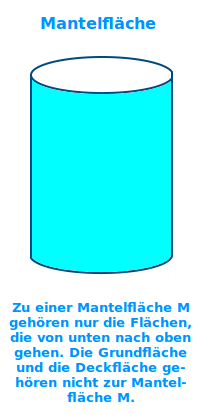
Mantelfläche
Definition
Die Fläche vom Boden bis zur Spitze oder bis zum Deckel eines 3D-Körper nennt man die Mantelfläche. => Ganzen Artikel lesen …
… heißt in der Mathematik oft => Grundfläche
Mathematik
Eine Unterfläche als Boden eines geometrischen Körpers heißt Grund- oder Bodenfläche. Bei Funktionsgraphen spricht man von einer Fläche unter der Kurve. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Grundfläche
Geometrie
Grundflächen gehören zu Körpern: sie sind diejenige Fläche, auf die man einen Körper normalerweise aufrecht stellen würde. Für spezielle Körper wie Kegel oder Zylinder sind die Grundflächen genau definiert. => Ganzen Artikel lesen …
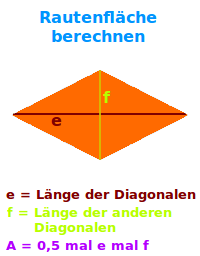
Rautenfläche berechnen
A = 0,5 mal e mal f
Länge e der einen Diagonalen mal Länge f der anderen Diagonalen und das Zwischenergebnis geteilt durch zwei ergibt den Flächeninhalt A der Raute. => Ganzen Artikel lesen …
… zum Beispiel in cm², siehe unter => Rautenfläche
A = 0,5·e·f
A ist der Flächenhalt, e und f sind die Längen der zwei Diagonalen. Dann gilt: A = 0,5 mal e mal f. Mehr unter => Rautenfläche berechnen
… Formel für den Flächeninhalt => Rautenfläche
