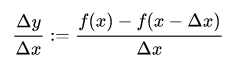Rückwärtsdifferenzenquotient
Definition Hilfspunkt liegt links von Bestimmungspunkt
Der Rückwärtsdifferenzenquotient gehört zur Bestimmung der Tangentensteigung oder der 1. Ableitung einer Funktion an einem Punkt P. Im sogenannten Sekantenverfahren wird dazu ein variabler Hilfspunkt Q gewählt, den man am Verfahrensende gegen P laufen lässt. Liegt der Hilfspunkt Q links vom Punkt P, entsteht daraus der Rückwärtsdifferenzenquotient. Siehe auch => Vorwärtsdifferenzenquotient
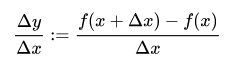Vorwärtsdifferenzenquotient
Definition: Hilfspunkt liegt rechts von Bestimmungspunkt
Der Vorwärtsdifferenzenquotient gehört zur Bestimmung der Tangentensteigung oder der 1. Ableitung einer Funktion an einem Punkt P. Im sogenannten Sekantenverfahren wird dazu ein variabler Hilfspunkt Q gewählt, den man am Verfahrensende gegen P laufen lässt. Liegt der Hilfspunkt Q rechts vom Punkt P, entsteht daraus der Vorwärtsdifferenzenquotient, er läuft auf der x-Achse nach rechts, also vorwärts. Siehe auch => Rückwärtsdifferenzenquotient
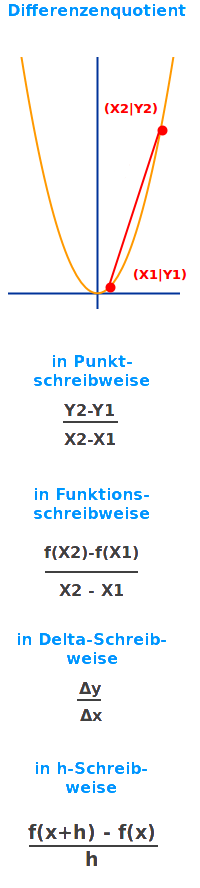
Differenzenquotient
Y2-Y1 durch X2-X1
Der Differenzenquotient dient der Berechnung der durchschnittlichen Steigung m zwischen zwei Punkten eines Graphen. Der Name kommt daher, dass man eine Differenz (Y2-Y1) durch eine andere Differenz (X2-X1) dividiert (Quotient). Eine kurze Schreibweise ist auch ΔY/ΔX, wobei das griechische Delta für Differenz steht. Er dient auch zum Berechnen der ersten Ableitung f'(x) über das Sekantenverfahren (h-Methode). => Ganzen Artikel lesen …
Sekantenverfahren
Das Verfahren liefert die erste Ableitung an einem Punkt für eine Funktion, also f'(x). Gebräuchliche Namen sind auch Ableiten über den Differentialquotienten oder die h-Methode. Das Verfahren ist ausführlich beschrieben unter => Sekantenverfahren
Altrnativen zu (Y2-Y1):(X2-X1)
(Y2-Y1):(X2-X1) - neben dieser Schreibweise gibt es noch viele weitere etwa mit Delta (δ, Δ), in Funktionsscheibweise oder speziell für die h-Methode (ableiten). Diese Versionen sind hier kurz aufgelistet. => Ganzen Artikel lesen …
