Geometrie
Ein Quader ist von der Form her eine rechteckige Kiste. Das Volumen von einem Quader, also das Quadervolumen, sagt, wie viel Raum (3D) der Quader einnimmt. Wenn der Quader ein Hohlraum ist, zum Beispiel ein Schwimmbadbecken, dann gibt das Volumen an, wie viel Wasser man dort hineinfüllen könnte. Berechnet wird das Volumen über Länge mal Breite mal Höhe, mehr unter => Quadervolumen berechnen
Geometrie
Ein Quadrat ist ein flaches Rechteck. Flache Sachen haben keinen Rauminhalt (Volumen). Flache Objekte können eine Länge oder Breite oder auch einen Flächeninhalt haben, abe kein Volumen. Hier stehen zwei Varianten was Quadratvolumen am ehesten meinen kann. => Ganzen Artikel lesen …
 Außenvolumen
Außenvolumen
Der gesamte Rauminhalt eines Körpers wie von außen gesehen
Ein Rohr hat ein Volumen, das es nach außen hin braucht. Das ist das Außenvolumen. Innen ist ein Rohr hohl. Der Hohlraum ist das Innenvolumen. Der Unterschied zwischen Außen- und Innenvolumen ist das Volumen der Rohrwand. => Ganzen Artikel lesen …
1425,5 Billionen km³
Nach der Sonne ist der Jupiter der größte Himmelskörper in unserem Sonnensystem. Er hat das rund tausendfache Volumen der Erde. Hier stehen die Zahlen dazu. => Ganzen Artikel lesen …
… meint am ehesten ein => Rechteck
 Oktaedervolumen
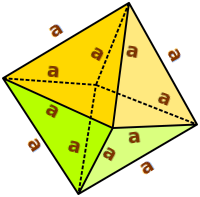
Oktaedervolumen
Formel
Ein Oktaeder sieht aus wie zwei aneinandergeklebten Pyramiden. Ein Oktaeder hat zwölf gleich lange Kanten. Ihre Länge heißt hier a. Hier stehen Formeln zur Berechnung des Volumens, also des Rauminhaltes. => Ganzen Artikel lesen …
 Quadervolumen berechnen
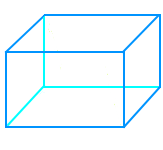
Quadervolumen berechnen
Anleitung
Eine rechteckige Kiste ist ein Beispiel für einen Quader. Man rechnet Länge mal Breite mal Höhe und erhält dann das Volumen eines Quaders, zum Beispiel in Kubikzentimetern (cm³) oder Kubikmetern (m³). Ein Quader, der 40 cm lang, 30 cm breit und 20 cm hoch ist hat ein Volumen von 24000 cm³ oder 24 Litern. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… Grundfläche G mal Höhe h, mehr unter => Quadervolumen

