f(x) = a·xⁿ
f(x) = 2x³ ist eine typische Potenzfunktion: als Potenzfunktion im engeren Sinn bezeichnet man jede Funktion, die man umformen kann in f(x) = Zahl·xⁿ. Das Dach ^ steht für hoch. Für das kleine n gibt es je nach Autor verschiedene Definitionen. Es steht jedoch immer für irgendeine Zahl (nie mit einer Variablen) außer der Zahl 0. Die 0 ist als Exponent nie erlaubt. Das ist hier näher vorgestellt. => Ganzen Artikel lesen …
Beispiele
f(x)=x oder f(x)=3x² oder auch f(x)=0,5x³ sind Potenzfunktionen der allgemeinen Form f(x) = a·xʳ. Je nachdem welche Zahlen für den Exponenten (Hochzahl) von x eingesetzt werden dürfen, unterscheidet man drei Arten von Potenzfunktion. Für alle drei Arten stehen hier konkrete Beispiele. => Ganzen Artikel lesen …
Kostenfunktion
BWL
Die Kostenfunktion gibt an, wie viel es kostet, eine bestimmte Menge zu produzieren: meistens versteht man unter einer Kostenfunktion eine Funktionsgleichung, die sagt, wie man für eine bestimmte zu produzierende Menge x die dazugehörigen Gesamtkosten y berechnet. Arten und Beispiele stehen unter => Kostenfunktionen
… ein anderes Wort für => ganzrationale Funktion
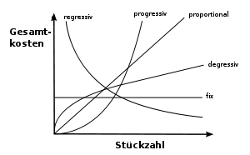Kostenfunktionen
Beispiele
Eine Kostenfunktionn stellt Kosten als Funktion der Stückzahl oder deren Änderungsrate dar. Dazu gibt es verschiedene Varianten, die hier kurz aufgelistet sind. => Ganzen Artikel lesen …
… ist am ehesten eine => ganzrationale Funktion
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
Übersicht
f(x)=ax^z hat als Graphen sogenannte Parabeln und Hyperbeln. Welche Art von Graph vorliegt, kann man anhand der Hochzahl (Exponent) von x entscheiden. Das ist hier erklärt. => Ganzen Artikel lesen …
… f(x) = a·xⁿ erlaubt für n nur natürliche Zahlen, mehr unter => Potenzfunktion
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
f(x)=x³ gibt abgeleitet f'(x)=3x²
Als Potenzfunktion bezeichnet man jede Funktion die man in die Form f(x)=a·x^r bringen kann. Die Definition welche Werte für r erlaubt sind ist nicht einheitlich. Für die Ableitungsregeln ist das aber unerheblich. Das kleine a darf jede beliebige reelle Zahl außer der Null sein. Zum Ableiten zieht man den Exponenten (die Hochzahl) als Faktor vor das x. Dann vermindert man den Exponenten um eins (rechnet ihn also minus eins). Die Zahl für a bleibt dabei unverändert erhalten. Aus x² wird so 2x. => Ganzen Artikel lesen …
f(x) = a·xⁿ
f(x) = 2x³ ist eine typische Potenzfunktion. Um sie aufzuleiten erhöhte man den Exponenten (die Hochzahl) um eins. Aus hoch-drei wird dann hoch-vier. Dann multiplziert man den ursprünglichen Funktionsterm noch mit 1 durch die neue Potenz, hier also mit 1/4. Die Aufleitung ist also F(x)=(1/4)·a^4. Die Grundidee dahinter ist das => Aufleiten über Potenzregel
… siehe unter => Potenzgleichung aus Versuch
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
f(x)=ax²
f(x)=ax² ist der Bauplan einer Potenzfunktion zweiten Grades. Das a darf irgendeine beliebige reelle Zahl außer der 0 sein. Eine konkrete Potenzfunktion ist zum Beispiel f(x) = 4x³. Diese Potenzfunktion ist gleichzeitig auch eine quadratische Funktion ohne lineares und ohne absolutes Glied. Der Funktionsterm alleine ist ein Monom. Zur Definition lies unter => Potenzfunktion
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
