Potenzen mit gleichem Exponenten
Vereinfachen
2³ und 4³: hier ist kurz vorgestellt, wie man zwei solche Potenzen addiert, subtrahiert, multipliziert oder dividiert. Man kann die Terme oft vereinfachen, aber nicht immer. => Ganzen Artikel lesen …
z. B. 2³ oder 5°
Potenzen sind Terme mit einem Exponenten (Hochzahl). Auf dieser Seite geht es um Arten und Beispiele von Potenzen. Eine Übersicht zum ganzen Thema steht unter => Potenzrechnung
Beispiele
Der Ausdruck 2 hoch 3 (kurz: 2³) heißt als ganzes Potenz. Die 2 ist die Basis, die 3 ist der Exponent. Der Exponent wird oft klein rechts oberhalb der Basis geschrieben und heißt deshalb auch Hochzahl. Hier stehen noch einige Beispiele. => Ganzen Artikel lesen …
… siehe unter => Potenzen mit gleichem Exponenten
… siehe unter => Potenzen mit gleichem Exponenten
Irgendwas hoch 0, 1, 2, 3 und so weiter
Solche Potenzen können als einfache Malkette gedacht werden => Ganzen Artikel lesen …
Anleitung
3³ + 2³ lässt sich nicht weiter zusammenfassen. Man rechnet, wenn möglich, erst beide Potenzen aus und addiert dann die Ergebnisse, was hier 35 gäbe. Es gibt aber einen Sonderfall, bei dem man weiter zusammenfassen kann. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
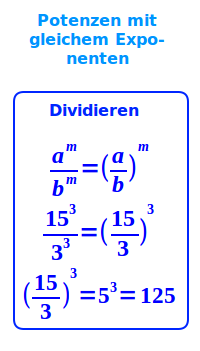Potenzen mit gleichem Exponenten dividieren
Vereinfachen
8³ durch 2³ gibt (8/2)³, also letztendlich 4³. Mit dieser Regeln lassen sich schwierige und unübersichtliche Terme oft stark vereinfachen. Dazu steht hier die allgemeine Regel mit Zahlenbeispielen. => Ganzen Artikel lesen …
Potenzen mit gleichem Exponenten multiplizieren
Vereinfachen
3² mal 4² gibt (3·4)² also letztendlich 12². Die allgemeine Regel lautet: a^m mal b^m wird (ab)^m. Das ist hier mit einem Zahlenbeispiel erklärt. => Ganzen Artikel lesen …
3³-2³
3³-2³ lässt sich nicht weiter vereinfachen, außer man rechnet erst die beiden Potenzen einzelnen aus. Das gäbe im Beispiel hier 27 minus 8, also als Endergebnis 19. Es gibt keine allgemeine Regel zum vereinfachen, aber einen Sonderfall, in dem es doch geht. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
