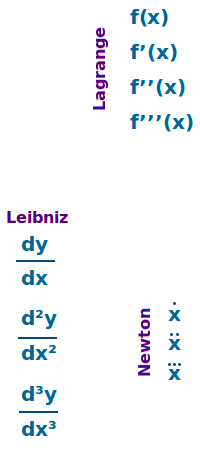Notationen von Ableitungen
Beispiele
f'(x), dy/dx oder ẋ sind drei Varianten die alle für die erste Ableitung stehen. Alle Varianten werden auch tatsächlich verwendet. Sie sind formal identisch haben aber gedanklich unterschiedliche Hintergründe. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Mathematik
Eine Notation ist eine fest geregelte Schreibweise. In der Mathematik und den Naturwissenschaften verwendet man Notationen um Dinge eindeutig, übersichtlich und vor allem kurz aufschreiben zu können. Hier stehen einige wichtige Beispiele dazu. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
Arten | Beispiele
Als Ableitung f'(x) bezeichnet man im erweiterten Sinn die Ableitungsfunktion zu einer gegebenen Funktion f(x). Man unterscheidet eine erste, zweite, dritte Ableitung etc. Ableitungen werden auch nach der Art der Ausgangsfunktion f(x) unterteilt. Auf dieser Seite stehen einige Beispiele. => Ganzen Artikel lesen …
… wie etwa f' oder f'', siehe unter => Notationen von Ableitungen
… siehe unter => Formelsammlung Differentialrechnung
… Die erste Ableitung f'(x) bilden, siehe unter => Ableiten
Ein Funktion f(x) abzuleiten heißt, dass man ihre Ableitungsfunktion f'(x) bestimmt. Beispiel: f(x) = 4x³ abgeleitet gibt f'(x) = 13x². Verfahren und Regeln unter => Ableiten
gibt: [cos(x)]^(-2), sprich: eins durch cosinus-quadrat-x
… x³ gibt abgeleitet 3x², mehr unter => ableiten über Potenzregel
