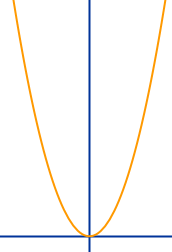
Normalparabel

Graph von y = x²

Die Normalparabel ist der Graph der Funktion f(x)=x². Statt f(x) wird oft auch y geschrieben, das meint dasselbe. Die Funktion f(x) = x² heißt auch Quadratfunktion. => Ganzen Artikel lesen …

4: A-normale Parabel

… z. b. eine kubische Parabel, siehe unter => keine normale Parabel

5: Unnormale Parabel

… z. b. eine kubische Parabel, siehe unter => keine normale Parabel

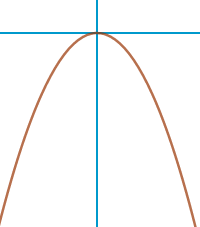Gespiegelte Normalparabel

Definition

Gespiegelt hießt für Graphen oft, dass sie an der x-Achse gespiegelt sind, das heißt: von oben nach unten oder von unten nach oben entlang der x-Achse umgeklappt. Das ist hier für die Normalparabel kurz erläutert. => Ganzen Artikel lesen …

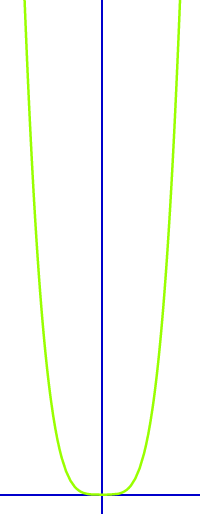
Kubische Normalparabel

Graph der Funktion f(x)=x³

Der Begriff „kubische Normalparabel“ ist in der Schulmathematik unüblich. Wir halten ihn aber als Analogie zur Normalparabel der quadratischen Funktion f(x)=x² für sinnvoll. Die kubische Normalparabel ist ein Sonderfall einer Parabel dritter Ordnung. => Ganzen Artikel lesen …

10: Minusnormalparabel

… Graph von f(x)=-Siehe unter => negative Normalparabel

11: Nach oben geöffnete Normalparabel

… der Graph von f(x)=x², heißt offiziell einfach nur => Normalparabel

12: Nach oben geöffnete Normalparabel

… Graph von f(x)=x², heißt einfach nur => Normalparabel

13: Nach unten geöffnete Normalparabel

… Graph von f(x)=-x², heißt meistens => gespiegelte Normalparabel

14: Negative Normalparabel

… ist nach unten geöffnet und heißt offiziell => gespiegelte Normalparabel

16: Normalparabel gekippt

… Graph von f(x)=-Siehe unter => negative Normalparabel

17: Normalparabel gespiegelt

… Graph von f(x)=-Siehe unter => negative Normalparabel

18: Normalparabel gespiegelt an x-achse

… Graph von f(x)=-Siehe unter => negative Normalparabel

19: Normalparabel im engeren Sinn

… ist nur der Graph von f(x)=x² und heißt einfach nur => Normalparabel

21: Normalparabel minus eins

… Graph von f(x)=-Siehe unter => negative Normalparabel

22: Normalparabel mit Maximum

… Graph von f(x)=-Siehe unter => negative Normalparabel

23: Normalparabel nach unten

… Graph von f(x)=-Siehe unter => negative Normalparabel

24: Normalparabel nach unten geöffnet

… Graph von f(x)=-Siehe unter => negative Normalparabel

25: Normalparabel negativ

… Graph von f(x)=-Siehe unter => negative Normalparabel

26: Normalparabel negative

… Graph von f(x)=-Siehe unter => negative Normalparabel

27: Normalparabel quartisch

… sieht aus wie eine normale Parabel, ist aber keine und heißt deshalb => Pseudonormalparabel

30: Nullstellen nach unten verschobener normalparabel

… siehe unter => Nullstellen von reinquadratischen Funktionen

31:

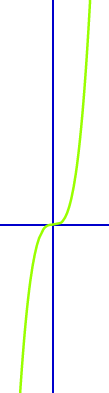
Pseudonormalparabel

Definition

Die Normalparabel ist definiert als der Graph der Funktion f(x)=x². Es gibt eine Reihe von anderen Funktionsgraphen die man beim Hinsehen kaum von einer Normalparabel unterscheiden kann. Diese kann man als Pseudonormalparabel bezeichnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

32:

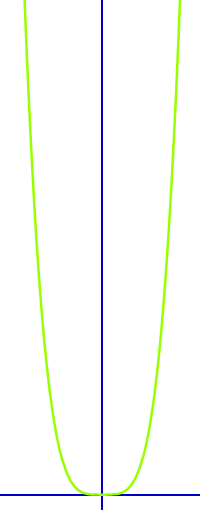Quartische Normalparabel

f(x)=x^4

Der Graph der Funktion f(x) gleich x-hoch-vier nennt man auch die quartische Normalparabel. Er sieht aus wie eine sehr stark gestreckte Normalparabel und ist nach oben geöffnet. Um seinen Scheitelpunkt verläuft sie fast wie eine waagrechte Gerade. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …

33: Scheinnormalparabel

… sieht aus wie eine normale Parabel, ist aber keine und heißt deshalb => Pseudonormalparabel

34: Umgedrehte Normalparabel

… also nach unten geöffnet, siehe unter => negative Normalparabel

35: Unechte Normalparabel

… sieht aus wie eine normale Parabel, ist aber keine und heißt deshalb => Pseudonormalparabel