Würfel, Quader, Prismen, Zylinder, Kegel
Die Mantelflächen sind anschaulich gesagt die senkrechten oder schräg nach oben gehenden Seitenflächen eines Körpers, wenn er auf der Grundfläche steht. Für verschiedene Körper gibt es angepasst Formeln, auf die hier verwiesen wird. => Ganzen Artikel lesen …
Wie man verschiedene Mantelflächen ausrechnet
Hier stehen einige Beispiele zur Mantelflächen. Häufig werden sie für oft vorkommende Standardkörper definiert. Eine allgemeine Definition steht unter => Mantelfläche
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
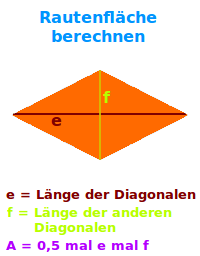
Rautenfläche berechnen
A = 0,5 mal e mal f
Länge e der einen Diagonalen mal Länge f der anderen Diagonalen und das Zwischenergebnis geteilt durch zwei ergibt den Flächeninhalt A der Raute. => Ganzen Artikel lesen …
Kugeln, Würfel, Quader, Pyramide etc.
Ein Würfel hat eine Oberfläche aber auch ein See oder ein Meer: Oberflächen können für 2D-Gewässeroberflächen oder für 3D-Körper berechnet werden. Beide Fälle werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Flächen berechnen
Über Formeln
Das Wort Fläche wird oft für Flächeninhalt verwendet. Mit Flächeninhalt meint man, wie groß eine Fläche ist. Anschaulich wäre das, wie viel Farbe man bräuchte, um die Fläche einmal anzupinseln. Flächeninhalte kann man zum Beispiel in Quadratzentimetern oder Quadratmetern angeben. Mehr zur Definition unter => Fläche
… ist r*s*Siehe unter => Kegelmantelfläche
M = ?
r·s·pi: der Kegelmantel ist die schräge Fläche. Wie groß ist der Inhalt, z. B. in cm²? Ein Lösungsweg steht unter => Kegelmantelfläche
