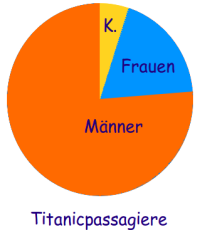
Kreisdiagramm
Definition
Ein Kreisdiagramm ist eine Darstellungsform für Teilwerte eines Ganzen als Tortenstücke eines Kreises. Die einzelnen Tortenstücke heißen mathematisch „Kreissektoren“. Jeder Sektor besteht aus zwei geraden Stücken und einem Kreisbogenteil am äußeren Rand. Die geraden Stücke heißen Schenkel. Sie treffen sich im Mittelpunkt des Kreises. Der Winkel zwischen den Schenkeln im Kreismittelpunkt heißt „Mittelpunktswinkel“. Seine Größe steht für die Zahl oder den Wert des entsprechenden Tortenstücks. Siehe auch => Kreisdiagramm zeichnen
=> Ganzen Artikel lesen …
… aus der Statistik, siehe unter => Boxplot
… nennt man eine => Kugel
… heißt in der Matrizenrechnung auch => Übergangsdiagramm
Umwandlung
Man soll als Kuchendiagram 3/4 von etwas darstellen. Wie viele Grad hat das entsprechende Kuchstück? Wie man das berechnet ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
Man soll das 0,15fache von einem Ganzen in einem Kreisdiagramm als Tortenstück (mathematisch: Kreissektor) darstellen. Wie groß muss der Winkel davon in Grad sein? Hier steht die Umrechnung. => Ganzen Artikel lesen …
Umwandlung
0,2 von einem Ganzen sollen in einem Kreisdiagramm als Tortenstück (Kreissektor) gezeichnet werden. Welchen Winkel nimmt man dafür? Hier steht ein Anleitung zur Umrechnen. => Ganzen Artikel lesen …
Umwandlung
Ein Tortenstück (Kreissektor) aus einem Kreisdiagramm hat einen Winkel an seiner Spitze, z. B. 40 Grad. Man schreibt das als Bruch mit dem Nenner 360 und hat dann 40/360. Diesen Bruch dann kürzen, hier zu 1/9. Das ist der Anteil des Tortenstücks am Gesamtkreis. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
45° ist wie
45° als Tortenstück (Sektor) von einem Kreis sind als Dezimal das 0,125fache vom ganzen Kreis. Die allgemeine Regel ist: Gradzahl durch 360 gibt Anteil als Dezimalzahl. Das ist hier mit Beispielen kurz erklärt. => Ganzen Artikel lesen …
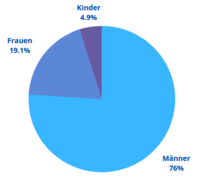Grad in Prozent für Kreisdiagramme
Umwandlung
In einem Kreisdiagramm ist ein Tortenstück (Kreissektor) mit einer Gradzahl angegeben. Dieses Tortenstück hat an seiner Spitze einen Winkel in Grad. Die Gradzahl durch 3,6 gibt immer die Prozentzahl für das Kreisdiagramm. Das ist hier mit Beispielen erklärt. => Ganzen Artikel lesen …
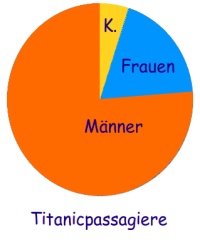Kreisdiagramm zeichnen
Anleitung | Titanicbeispiel | Aufgaben
Ein Kreisdiagramm besteht meist aus einem Kreis, der in tortenstückartige Teile aufgeteilt wird. Diese Stücke heißen auch Sektoren oder Kreisausschnitte. Hier wird an einem Beispiel (Titanic) erklärt, wie man ein Kreisdiagramm in der Statistik zeichnet. => Ganzen Artikel lesen …
… Anleitung, Tipps und Übungsdaten unter => Kreisdiagramm zeichnen
Umrechnung
30 % sollen in einem Kreisdiagramm eingezeichnet werden. Hier steht, wie man das in eine Dezimalzahl umrechnet und dann damit den passenden Winkel (im Beispiel 108°) für das Kreisdiagramm berechnet. => Ganzen Artikel lesen …
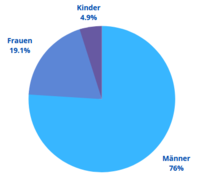Prozent in Grad für Kreisdiagramme
Rechnung und Tabelle
40 % gibt 144° als Winkel für das Tortenstück im Kreisdiagramm: man nimmt die Zahl vor dem Prozentzeichen, teilt sie durch hundert und rechnet dann das Zwischenergebnis mal 360. Das Ergebnis ist dann die gesuchte Gradzahl. Das ist hier noch kurz mit Beispielwerten erklärt. => Ganzen Artikel lesen …
… siehe unter => Prozent in Grad für Kreisdiagramme
… siehe unter => Grad in Prozent für Kreisdiagramme
