Integrationsintervall
Definition
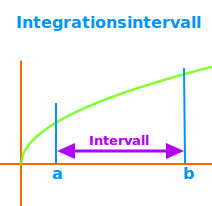
Als Integrationsintervall bezeichnet man alle x-Werte von der linken bis zur rechten Integrationsgrenze. Es ist also der Bereich der x-Achse für das man das Integral einer Funktion bestimmen möchte. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… meistens von a bis b, siehe unter => Integrationsintervall
… für verschiedene Funktionstypen, siehe unter => aufleiten
Das dx in ∫f(x)·dx
∫f(x)·dx liest man als: Das Integral von f(x). Das dx ist dabei das sogenannte Differential. Anschaulich steht es für die Breite einer Säule, die man im Rahmen der Säulenmethode zur Berechnung der Fläche zwischen Graph und x-Achse verwendet. Die Bedeutung des Integrationsdifferentials ist anschaulich erklärt im Artikel zum => Integralzeichen
… oft ein kleines b, meint dasselbe wie => Rechte Integrationsgrenze
… oft ein kleines a, meint dasselbe wie => Linke Integrationsgrenze
