 HO
HO
Modelleisenbahn | Chemie | H₀
Ein großes H gefolgt von einem kleinen oder großen o: das kann ein Maßstab für Modelleisenbahnen oder das chemische Element Holmium sein. Daneben gibt es noc weitere Bedeutungen. => Ganzen Artikel lesen …
Chemie
Co mit kleinem o steht für das chemische Element Cobalt. CO mit großem O steht für das chemische Molekül Kohlenmonoxid und CO2 für das Treibhausgas Kohlendioxid. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Do
Do
Programmieren
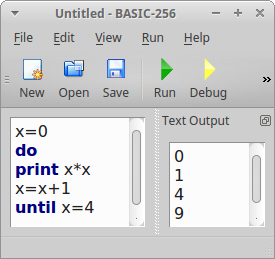
Do - als englisches Wort im Sinne von tue, mache - leitet in vielen Programmiersprachen eine Schleife ein. Siehe zum Beispiel => Basic256 do until
Bedeutungen
Als kleines h oder als großes H: der lateinische Buchstabe kann für verschiedene Dinge stehen, hier stehen Beispiele aus der Mathematik und den Naturwissenschaften. => Ganzen Artikel lesen …
… Abkürzung für die World Health Organisation der => UNO
 Rho
Rho
ρ, Ρ
Das kleine Rho ρ und das große Ρ bilden de siebzehnten Buchstaben im griechischen Alphabet. Während das kleine Rho (ρ) eine wichtige Rolle in der Physik und Chemie spielt, wird das große Rho (P) kaum als Formelzeichen verwendet. Beide Buchstaben sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… als griechische Silbe: Weg, siehe als Beispiel das => Hodometer
Gibt (meistens): 1
Irgendein Term hoch 0 ergibt immer die Zahl 1. Außer, wenn die Basis, hier also a+b selbst die Zahl 0 ergibt. Dann ist der Term nicht definiert. Mehr dazu unter => binomische Formel hoch 0
Gibt: a+b
Irgendein Term hoch 1 meint, dass der Term selbst unverändert bleibt. Hoch 1 kann man weglassen, ohne dass sich der Wert des Terms dadurch verändert. (a+b)¹ ist wie (a+b) oder einfach nur a+b. Siehe auch => binomische Formel hoch 1
Gibt: a² + 2ab + b²
(a+b)² ist wie (a+b)·(a+b). Multipliziert man die Klammern aus, dann erhält man a² + 2ab + b². Das entsprechende Rechengesetz ist die => erste binomische Formel
Gibt: a³ + 3a²b + 3ab² + b³
(a+b)³ ist wie (a+b)·(a+b)·(a+b). Multipliziert man die Klammern aus, dann erhält man a(a+b)³ = a³ + 3a²b + 3ab² + b³. Mehr dazu unter => binomische Formel hoch 3
Gibt: a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
(a+b)⁴ ist wie (a+b)·(a+b)·(a+b)·(a+b). Multipliziert man die Klammern aus, dann erhält man a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴. Mehr dazu unter => binomische Formel hoch 4
Gibt: a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵
(a+b)⁵ ist wie (a+b)·(a+b)·(a+b)·(a+b)·(a+b). Multipliziert man die Klammern aus, dann erhält man a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵. Mehr dazu unter => binomische Formel hoch 5
… gibt a³+3a²b+3ab²+b³, mehr dazu unter => binomischer Lehrsatz
… siehe dazu unter => (a+b)^n
Gibt: a² - 2ab + b²
(a-b)² ist wie (a-b)·(a-b). Multipliziert man die Klammern aus, dann erhält man a² - 2ab + b². Das entsprechende Rechengesetz ist die => zweite binomische Formel
… gibt a³-3a²b+3ab²-b³, mehr dazu unter => binomischer Lehrsatz
… gibt a³-3a²b+3ab²-b³, mehr dazu unter => binomischer Lehrsatz
… gibt x³+3x²y+3xy²+y³, mehr dazu unter => binomischer Lehrsatz
… gibt x³+3x²y+3xy²+y³, mehr dazu unter => binomischer Lehrsatz
… gibt x³-3x²y+3xy²-y³, mehr dazu unter => binomischer Lehrsatz
… gibt x³-3x²y+3xy²-y³, mehr dazu unter => binomischer Lehrsatz
… 0 hoch hoch irgendwas gibt fast immer 0, mehr unter => Null hoch
… warum das nicht definiert ist, siehe unter => Null hoch minus eins
… warum das nicht definiert ist, siehe unter => Null hoch minus zwei
… nicht definiert, mehr unter => null hoch null
… ergibt genau 0, mehr unter => null hoch
… egal was, ist nicht definiert, siehe auch => Null hoch minus eins
… warum das nicht definiert ist, siehe unter => Null hoch minus eins
… warum das nicht definiert ist, siehe unter => Null hoch minus zwei
… warum das nicht definiert ist, siehe unter => Null hoch minus eins
… warum das nicht definiert ist, siehe unter => Null hoch minus zwei
Genau 0
Denn: 0-hoch-2 ist ausgechrieben eine Malkette aus Nullern (Basis), und zwar genau 2 davon (Hochzahl). Ausgeschrieben gibt das: 0·0. Und 0 mal 0 gibt wieder 0. Siehe mehr dazu unter => null hoch
Genau 10000
Genau 10000

