Geometrie
Gedachte Linie auf der ein Dreieck aufrecht steht: stelle dir ein Dreieck aus dicken Holz vor. Es liegt flach auf dem Tisch. Jetzt stellst du es mit irgendeiner seiner drei schmalen Seiten aufrecht auf den Tisch. Aufrecht heißt hier, dass das Dreieck wie eine kleine Maür stehen soll. Die Seite auf der es steht nennt Grundlinie. Da man ein Dreieck auf jede seiner drei schmalen Seiten stellen kann, hat ein Dreieck auch drei verschiedene Grundlinien. Siehe auch => Dreieckshöhe
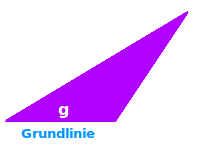Grundlinie
A = ½·g·h
In Flächenformeln tritt oft das Wort Grundlinie oder Grundseite auf, oft abgekürzt mit einem kleinen g. Hier wird kurz erklärt, was g bedeutet. => Ganzen Artikel lesen …
Definition: berührt eine Dreiecksseite und die Verlängerung der zwei anderen Seiten
Ein Ankreis ist ein Kreis, der von einer Dreiecksseite von außen und von den Verlängerungen der beiden anderen Seiten tangential berührt wird. Jedes beliebige Dreieck besitzt genau drei Ankreise. Die Ankreismittelpunkte liegen jeweils auf der Winkelhalbierenden eines Innenwinkels und auf den Winkelhalbierenden der beiden Außenwinkel, die nicht zu dem Innenwinkel gehören. => Ganzen Artikel lesen …
Geometrie
der Inkreis eines Dreiecks berührt jede Seite des Dreiecks genau einmal von innen: den Mittelpunkt des Inkreises findet man, indem man die drei Winkelhalbierenden des Dreiecks konstruiert. Dort wo sie sich alle drei schneiden, dort liegt der Mittelpunkt des Inkreises. Den Radius des Inkreises findet man, indem man ein Lot vom Mittelpunkt auf eine der Seiten fällt. Die Verbindungsstrecke vom Mittelpunkt zum Schnittpunkt des Lots mit der Seite ist der Radius. Siehe auch => Winkelhalbierende
… gibt es nicht wirklich, mehr unter => Dreiecksmittelpunkt
… gibt es nicht, warum nicht steht unter => Dreiecksdiagonale
… gibt es nicht, warum nicht steht unter => Dreiecksdiagonale
