==== Übersicht ====
Siehe auch => Ganzen Artikel lesen …
 AE
AE
Etwa 150 Mio. km
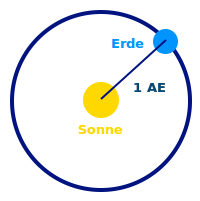
Eine 150000000 Kilometer: eine astronomische Einheit ist der ungefähre Abstand der Erde zur Sonne, rund 150 Millionen Kilometer. Lies mehr unter => Astronomische Einheit
… mit der Ordnungszahl 4, das Element => Beryllium
Mathematik | Physik | Chemie
Eulersche Zahl, Elektronenladung, Gleitzahl etc.: das kleine e steht für verschiedene Bedeutungen. => Ganzen Artikel lesen …
Forty-foot equivalent Unit
Die Forty-foot equivalent Unit ist eine Standardgröße für einen Container. 40 Foot bezieht sich dabei auf die Länge (etwa 12 Meter). Lies mehr dazu unter => Standardcontainer
… Magnetit => Eisen(ii,iii)-Oxid
 Ufer
Ufer
Randbereich von Gewässern
Das Ufer ist der Landbereich direkt nahe an einem Gewässer. Von einem Ufer spricht man meist bei Binnengewässern wie Flüssen, Seen oder Teichen. Am Meer spricht man eher von der Küste. => Ganzen Artikel lesen …
… chemische Summenformel für das Mineral => Olivin
… ist die chemische Summenformel für => Olivin
… etwa 2 Gramm schwer, mehr unter => Ein-Pfennig-Münze
… wiegt etwa 4 Gramm, siehe auch => Zehn-Pfennig-Münze
… gab es nicht, wäre vom Wert her dasselbe gewesen wie eine => D-Mark
… mit Punkten oder anderen Zeichen, siehe unter => Hunderterfeld
… die Zahlen 1 bis 100 => Hunderterfeld
… mit Zahlen von 1 bis 100, siehe unter => Hundertertafel
Die alten Cents, zu DM-Zeiten
10 Pfennige gab es als eine Münze. Sie wog etwa 4 Gramm. 10 Pfennige nannte man früher auch einen Groschen. => Ganzen Artikel lesen …
Die alten Cents, zu DM-Zeiten
10 Pfennige gab es als eine Münze. Sie wog etwa 4 Gramm. 10 Pfennige nannte man früher auch einen Groschen. Siehe auch unter => D-Mark
… Anzahl Einser bei Wurf mit 12 Würfeln, siehe unter => Zwölf-Würfel-Versuch
… wog 3,25 Gramm, mehr unter => Zwei-Pfennig-Münze
… siehe unter => zweihundert-Würfel-Versuch
Würfel?
Ein Würfel ist immer ein Körper, also dreidimensional (3D). Ein 2D-Würfel ist also ein Widerspruch in sich selbst. => Ganzen Artikel lesen …
… wog 3 Gramm, mehr unter => Fünf-Pfennig-Münze
… wog 3,5 Gramm, mehr unter => Fünfzig-Pfennig-Münze
…. siehe unter => Orthogonalität überprüfen
… Der höchste ist mit 133 Metern der => Mulleklenkes
In Aachen und Umgebung gibt es mehrere Fernmeldetürme (in Betrieb und stillgelegt). Der größte und weithin sichtbare ist der Mulleklenkes. Sehr viel kleiner ist der benachbarte Fernmeldeturm Kronprinzenrast. Lies mehr unter => Mulleklenkes
… Abschreiben, nachmachen, imitieren oder => kopieren
… im Wechsel der Gezeiten an Küsten die => Ebbe
f'(x)
f(x) = x²-4x gibt abgeleitet f'(x) = 2x-4. Bei einer Differenz kann man die einzelnen Glieder auch einzeln für sich ableiten. Das Vorgehen ist genau so wie beim => Ableiten über Summenregel
Sekantenverfahren
Das Verfahren liefert die erste Ableitung an einem Punkt für eine Funktion, also f'(x). Gebräuchliche Namen sind auch Ableiten über den Differentialquotienten oder die h-Methode. Das Verfahren ist ausführlich beschrieben unter => Sekantenverfahren
… jedes Glied einzeln ableiten, mehr unter => Ableiten über Summenregel
… f(x)=5x³-x² gibt f'(x)=15x²-Siehe unter => ableiten über Summenregel
… jedes Glied einzeln ableiten, mehr unter => Ableiten über Summenregel
… jedes Glied einzeln ableiten, mehr unter => Ableiten über Summenregel
dx:dy
Sowohl dx als auch dy nennt man hier ein Differential. Differentiale sind beliebig klein gedachte Unterschiede von Werten, etwa von x- oder y-Werten. In dem Term dy/dx sind sowhl der Zähler als auch der Nenner ein Differential. Der gesamte Term ergibt als Grenzwert die erste Ableitung f'(x). => Ganzen Artikel lesen …
… Tabelle von +50 bis -25 Grad Celsius unter => Luftfeuchtigkeiten

