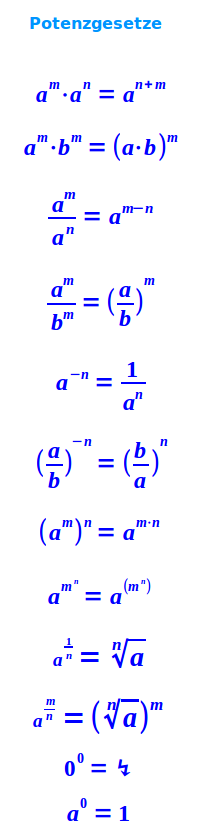Potenzgesetze

Kurzversion

Basiswissen

aᵐ·aⁿ

• Regel: aᵐ·aⁿ = aᵐ⁺ⁿ
  

• Man multipliziert zwei Potenzen mit gleicher Basis:
  

• Basis zusammenfassen, Exponenten addieren: 2³·2²=2⁵
  

• Mehr unter => Potenzen mit gleicher Basis multiplizieren
  

aᵐ:aⁿ

• Regel: aᵐ:aⁿ = aᵐ⁻ⁿ
  

• Man dividiert zwei Potenzen mit gleicher Basis:
  

• Basis zusammenfassen, Exponenten subtrahieren: 5³:5²=5¹
  

• Mehr unter => Potenzen mit gleicher Basis dividieren
  

aᵐ·bᵐ

• Regel: aᵐ·bᵐ = (a·b)ᵐ
  

• Man multipliziert zwei Potenzen mit gleichem Exponenten
  

• Basen multiplizieren, Exponenten zusammenfassen: 4³·2³=8³
  

• Mehr unter => Potenzen mit gleichem Exponenten multiplizieren
  

aᵐ:bᵐ

• Regel: aᵐ:bᵐ = (a:b)ᵐ
  

• Man dividiert zwei Potenzen mit gleichem Exponenten
  

• Basen dividieren, Exponenten zusammenfassen: 10³:5³=2³
  

• Mehr unter => Potenzen mit gleichem Exponenten dividieren
  

r⁻ᵐ

• Regel: (a:b)⁻ᵐ = (b:a)ᵐ
  

• Die Basis immer erst als Bruch schreiben.
  

• Die Zahl 8 kann man zum Beispiel schreiben als: 8/1
  

• Minus weglassen, dafür Kehrwert von Basis bilden
  

• Mehr unter => Negativer Exponent
  

(aᵐ)ⁿ

• Regel: (aᵐ)ⁿ = aᵐⁿ
  

• Eine Potenz wird als Ganzes wieder potenziert.
  

• Basis gleichlassen, Exponenten multiplizieren: (2³)² = 2⁶
  

• Mehr unter => Potenzen potenzieren
  

Potenzturm

• 2^3^4 = 2^81
  

• Immer von rechts rechnen
  

• Erst 3⁴ (gibt 81), dann 2⁸¹
  

• Mehr unter => Potenzturm
  

∜a

• Regel: n-te Wurzel aus a = a^(1/n)
  

• n-te Wurzel aus a = a hoch eins-durch-n
  

• Mehr unter => n-te Wurzel aus Potenz
  

• Mehr unter => r-te Wurzel aus Potenz
  

a⁰

• Regel a⁰=1 für alle a≄0
  

• Mehr unter => Hoch Null
  

0⁰

• Regel: 0⁰=↯
  

• Ist nicht definiert (geht nicht)
  

• Mehr unter => Null hoch Null
  

Auf- und ableiten

• x² aufgeleitet gibt x³/3 => Aufleiten über Potenzregel
  

• x² abgeleitet gibt 2x => Ableiten über Potenzregel
  

Tipp

Aufgaben dazu