Kiste 17 Versuch Leiterstellhöhe
🚒 Anleitung
Basiswissen
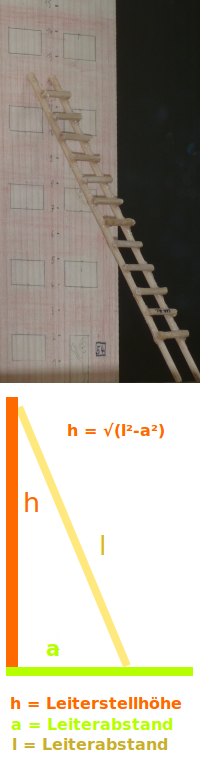
Eine Leiter mit einer bekannten und festen Länge l wird schräg an eine Hauswand gelehnt. In welcher Höhe h lehnt sie oben an, wenn man sie unten horizontal einen bestimmten Abstand a vom Haus hat? Das wird hier praktisch betrachtet.
Schritt 1:
Blatt anlegen: Nimm ein DIN-A4-Blatt und lege es hochkant vor dich. Lasse gleich beim Schreiben links immer einen Rand. Der Rand soll ungefähr so lang sein wie ein halber Zeigefinger (5 cm sind gut). Schreibe oben groß als Überschrift: "Kiste 17 Versuch Leiterstellhöhe". Ganz unten auf das Blatt schreibst du deinen Namen und das Datum von heute. Jetzt kommt die Versuchsskizze: zeichne links auf das Blatt eine senkrechte Linie von 16 Zentimetern Länge. Am unteren Rand dieser senkrechten Linie zeichnest du jetzt eine waagrechte Linie von 15 Zentimetern Länge. Insgesamt entsteht so ein großes L von 16 cm Höhe und 15 cm Breite.
Schritt 2:
Vorbereitung: Hole die Kiste 17 und stelle sie auf den Tisch. Nimm heraus: Das Holzstück mit dem gemalten Haus, die lange Pappe und die kleine Holzleiter. Mehr brauchst du nicht. Die Kiste kannst du dann wegstellen. Die Pappe aus der Kiste hat zwei Seiten. Auf einer Seite ist ein langes Rechteck gezeichnet. In ihm steht, dass du dort das Haus stehen soll. Stelle dort das Holzhaus aus der Kiste auf.
Schritt 3:
Vorversuch: Auf der Pappe siehst du vom Haus weggehend eine Skala mit Zahlen von 1 bis 14. Die Zahlen sind der Abstand vom Haus an dieser Stelle in Zentimetern. Stelle die Leiter bei genau 9 Zentimetern vom Haus entfernt auf den Boden. Diesen Abstand nennen wir den "Leiterabstand", kurz: l. Lehne die Leiter dann an das Haus an. Auf dem Haus ist auch eine Zahlenskala. Die Zahlen am Haus stehen für die Höhe über dem Boden in Zentimetern. Wenn du alles richtig gemacht hast, dann sollte die Leiter in einer Höhe von etwa 11 cm am Haus lehnen. Diese Höhe nennen wir die "Leiterhöhe", kurz: h.
Schritt 4:
Skizze: Übertrage diese Leiterposition in die Skizze auf das Blatt Papier. Zeichne die Leiter als Strich vom Boden (9 cm vom Haus entfernt) bis zur Hauswand (bei 11 cm Höhe) ein. Schreibe an die Bodenseite: "Leiterabstand a etwa 9 cm". Schreibe an die Hausseite: "Leiterhöhe h etwa 11 cm." Schreibe an die Leiter: "Leiterlänge l etwa 14 cm".
Schritt 5
Tabelle: Lege rechts von der Skizze eine senkrechte Tabelle mit zwei Spalten an. Die erste Spalte kriegt die Überschrift "a in cm". Die zweite Spalte hat die Überschrift "h in cm". Schreibe in der ersten Spalte von oben nach unten die Zahlenwerte von 0 bis 14.
Schritt 6
Versuch: Stelle nun die Leiter bei all diesen Abständen vom Haus auf den Boden. Notiere in der Tabelle die jeweils dazu gehörenden Höhen h. Schätze dabei die Millimeter zwischen den ganzen Zentimetern nach Augenmaß. Wenn die Tabelle insgesamt 15 Wertepaare hat, dann bist du fertig mit dem Versuch.
Nicht proportional
Dieser Versuch führt zu einer nicht proportionalen Zuordnung oder Funktion: Man hat eine proportionale Funktion oder Zuordnung, wenn folgendes immer stimmt: verdoppelt man den x-Wert, dann verdoppelt sich immer auch der y-Wert. Der x-Wert wäre hier der Abstand a der Leiter vom Haus und y die Höhe h der Leiter über dem Boden. Wenn man nun den Abstand vom Haus von von 2 auf 4 cm verdoppelt, dann verdoppelt sich der y-Wert nicht. Im Gegenteil: er nimmt sogar ab. Damit handelt es sich hier sicher nicht um eine proportionale Zuordnung oder Funktion. Woran man etwas Proportionales erkennt ist erklärt auf Proportionaliät erkennen (externer Link)
Funktionsgleichung aufstellen
Es gibt eine Formel, mit der man aus einen bekannten Abstand a der Leiter vom Haus direkt die Anlehnhöhe h der Leiter berechnen kann. Allgemein hat die Formel die Form h = f(a). Das heißt: h = irgendein Term mit a. Um einen passenden Term zu finden, kann man den Satz des Pythagoras verwenden. Man kann das Ergebnis selbst überprüfen, indem man am Ende alle im Versuch ermittelten Werte von a einsetzt und vergleicht, ob die Formel die passenden Werte für h ergibt. Erste Tipps dazu stehen unter Funktionsgleichung aus Versuch ↗