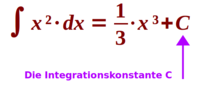Integrationskonstante
C
Kurzinfo
f(x) = 4x gibt aufgeleitet F(x) = 2x² + C. Das C am Ende ist eine reine Zahl ohne x und heißt Integrationskonstante. Diese Integrationskonstante fällt beim Ableiten von F(x) wieder weg, wird also zu 0. Das ist hier kurz erklärt.
Sinn der Integrationskonstanten C
Jede Funktion, die abgeleitet wieder f(x) gibt, ist eine sogenannte Stammfunktion von f(x). Wenn man die Grundfunktion f(x) = 2x betrachtet, dann kann man dazu viele verschiedene, aber untereinander ähnliche Stammfunktionen F(x) finden. Hier sind einige Beispiele:
- F(x) = 2x² + 20 ⭢ abgeleitet ⭢ f(x) = 4x ✔
- F(x) = 2x² + 99 ⭢ abgeleitet ⭢ f(x) = 4x ✔
- F(x) = 2x² - 12 ⭢ abgeleitet ⭢ f(x) = 4x ✔
- F(x) = 2x² - 11 ⭢ abgeleitet ⭢ f(x) = 4x ✔
Erklärung
Man erkennt an den Beispielen oben: man kann am Ende eine beliebige Zahl plus oder minus rechnen, also zum Funktionsterm addieren oder von ihm subtrahieren. Eine solche Zahl nennt man eine Kontante. Da beim Ableiten konstante Zahlen wegfallen, haben sie keinen Einfluss auf die Ableitung. Man kann also bei einer Stammfunktion am Ende eine beliebige Zahl mit + oder - anfügen. Für diese beliebige Zahl steht die Integrationskonstante C. Siehe auch Aufleitungsregeln ↗
Muss sie immer mitgeschrieben werden?
Nein. Wenn man nur irgendeine Stammfunktion angeben soll, dann kann man die Integrationskonstante weglassen. Man schreibt dann: f(x) = 4x gibt aufgeleitet F(x) = 2x. Groß F(x) ist dann aber nur eine theoretisch unendlich vielen Stammfunktionen. Soll das verdeutlicht werden, schreibt man das + C am Ende mit auf. Siehe auch Stammfunktion ↗