Extremwertaufgaben über Analysis
Lösungsschema
Basiswissen
Extremwertaufgaben sind spezielle Optimierungsaufgaben. Man kann sie oft über die 1. und 2. Ableitung lösen. An einem gerechneten Beispiel wird ein Lösungs-Schmema erklärt, dass für fast alle Aufgaben von diesem Typ ein Ergebnis liefert. Das Verfahren geht über 6 Schritte.
1. Zielgröße festlegen
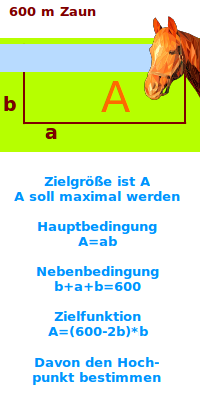
- Die Zielgröße ist das, was mini- oder maximal werden soll.
- Buchstaben für die Zielgröße festelegen, z. B. ein großes A für eine Fläche.
- Irgendeine eine flache Fläche, z. B. Rechteck: A
- Von einem Körper, z. B. Quader, die Oberfläche: O
- Von einen Körper, z. B. Zylinder, das Volumen: V
- Siehe auch Zielgröße ↗
2. Hauptbedingung aufstellen
- Die Hauptbedingung ist eine Formel.
- Links vom Gleichzeichen steht nur die Zielgröße.
- Rechts steht eine Formel, wie man die Zielgröße berechnen könnte.
- Diese Formel darf rechts mehrere Unbekannte haben.
- Umgebe jede einzelne Unbekannte mit einer Klammer.
- Siehe auch Hauptbedingung ↗
0. Zwischengedanke
- Gleich soll die Zielfunktion erstellt werden.
- Die Zielfunktion ist wie die Hauptbedingung, aber sie darf rechts nur eine Unbekannte stehen haben.
- Dass rechts vom Gleichheitszeichen nur noch eine Unbekannte steht ist das Ziel der Nebenbedingung.
- Hat die Hauptbedingung rechts bereits nur eine Unbekannte, dann ist die Hauptbedingung bereits die Zielfunktion.
- In diesem Fall kann man direkt zum Punkt 5 weitergehen.
3. Nebenbedingung aufstellen
- Man nimmt die rechtsseitigen Unbekannten der Hauptbedingung.
- Man sucht und formuliert irgendeine formelhafte Beziehung zwischen ihnen.
- Man sucht also eine Formel, in der die Unbekannten vorkommen.
- Diese Formel nennt man dann die Nebenbedingung.
- Die Nebenbedingung jetzt nach irgendeiner der Unbekannten umstellen
- Umstellen meint: diese Unbekannte steht am Ende links alleine.
- Siehe auch Nebenbedingung ↗
4. Zielfunktion aufstellen
- Man verbindet jetzt Haupt- und Nebenbedingung über das Einsetzungsverfahren ↗
- Man setzt dazu den Term rechts aus der umgestellen Nebenbedingung für die ...
- entsprechende Unbekannte aus der Hauptbedingung ein.
- Jetzt hat man rechts in der Hauptbedingung nur noch eine Unbekannte.
- Ab jetzt heißt die Hauptbedingung dann Zielfunktion.
- Siehe auch Zielfunktion ↗
5. Globale Extrempunkte bestimmen
- Wenn man die Zielfunktion hat, dann bestimmt den Definitionsbereich:
- Lege den kleinsten sinnvoll möglichen Wert für die Unbekannte fest.
- Lege den größten sinnvoll möglichen Wert für die Unbekannte fest.
- Der Definitionsbereich sind alle Zahlen vom kleinsten bis größten Wert.
- Dann bilde von der Zielfunktion die erste Ableitung f'(x)
- Globalen Hoch- oder Tiefpunkt (je nach Fragestellung) bestimmen.
- Global meint hier: innerhalb des gesamten Definitionsbereiches.
- Für Maxima siehe Globalen Hochpunkt bestimmen ↗
- Für Minima siehe Globalen Tiefpunkt bestimmen ↗
- Als Ergebnis hat man dann eine Extremstelle.
- Das ist der x-Wert der Unbekannten.
6. Restliche Unbekannte bestimmen
- Man nimmt den Wert der in 5 bestimmten Unbekannten.
- Man setzt ihn in die Nebenbedingung ein.
- Man stellt die Nebenbedingung um nach der anderen Unbekannten.
- Damit kann man ihren Wert bestimmen.
7. Extremwert bestimmen
- Die Werte alle Unbekannten setzt man jetzt in die Hauptbedingung ein.
- Das gibt den gesuchten Extremwert (maximal oder minimal) der Zielgröße.
8. Antwort
- Man schreibt die gefundenen Werte für die Unbekannten ...
- und für die Zielgröße in einem Antwortsatz auf.
Wo steht ein Zahlenbeispiel?
- Das Standardbeispiel ist die Maximierung einer Weidefläche.
- Es ist vorgerechnet auf Weideflächenmaximierung über Hochpunkt ↗
Aufgaben zur Übung
- Extremwertaufgaben können extrem schwer zu lösen sein.
- Eine Sammlung mit Lösungen ist hier als Quickcheck zusammengestellt.
- Zu den Aufgaben geht es über => qck